
科目: 来源: 题型:
【题目】如图:
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)请计算△ABC的面积;
(3)直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标.

查看答案和解析>>
科目: 来源: 题型:
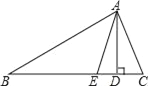
【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度数;
(2)写出∠DAE与∠ACB﹣∠ABC的数量关系: ,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D在边AC上,下列条件中,能判断△BDC与△ABC相似的是 ( )

A. AB·CB=CA·CD B. AB·CD=BD·BC C. BC2=AC·DC D. BD2=CD·DA
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,D、E、F、G四点在△ABC的三边上,其中DG与EF相交于点H.若 ∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是( )
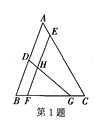
A.△BDG,△CEF B.△ABC,△CEF C.△ABC,△BDG D.△FGH,△ABC
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
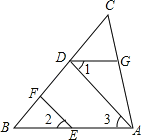
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= (等量代换)
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵∠CAB=70° ,(已知)
∴∠AGD= (等式性质)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
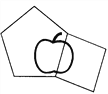
A. 4 B. 3 C. 6 D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(___ ___)
∴∠2=∠CGD(等量代换)
∴CE∥BF(__ ___)
∴∠____ ____=∠BFD(___ ____)
又∵∠B=∠C(已知)
∴____ ____(等量代换)
∴AB∥CD(___ ____)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com