科目： 来源： 题型：
【题目】已知关于x的方程x2﹣（m+2）x+2m﹣1=0．
（1）求证：此方程有两个不相等的实数根；
（2）若抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；
（3）填空：若x2﹣（m+2）x+2m﹣1=0的两根都大于1，则m的取值范围是 ．
查看答案和解析>>
科目： 来源： 题型：
【题目】去学校食堂就餐，经常会在一个买菜窗口前等待，经调查发现，同学的舒适度指数y与等时间x（分）之间满足反比例函数关系，如下表：
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
（1）求y与x的函数关系式，并写出自变量x的取值范围．
（2）若等待时间8分钟时，求舒适度的值；
（3）舒适度指数不低于10时，同学才会感到舒适．请说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E，如果∠BAC=60°，∠ACE=24°，那么∠BCE的大小是（ ）
A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目： 来源： 题型：
【题目】如图,在等边三角形ABC中,已知点O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
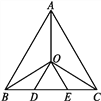
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，AB∥CD，∠BAC与∠DCA的平分线相交于点G，GE⊥AC于点E，F为AC上的一点，且FA＝FG＝FC，GH⊥CD于H.下列说法：①AG⊥CG；②∠BAG＝∠CGE；③S△AFG＝S△CFG；④若∠EGH︰∠ECH＝2︰7，则∠EGF＝50°.其中正确的有（ ）
A. ①②③④ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在平面直角坐标系中，点O为坐标原点，点
在第一象限，过点A向x轴作垂线，垂足为点B，连接OA，
，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN．
求a的值；
当
时，
请探究
，
，
之间的数量关系，并说明理由；
试判断四边形AMON的面积是否变化？若不变化，请求出其值；若变化，请说明理由．
当
时，请求出t的值．
查看答案和解析>>
科目： 来源： 题型：
【题目】某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图． 最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
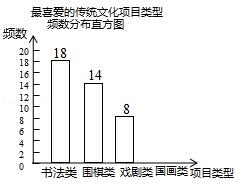
根据以上信息完成下列问题：
（1）频数分布表中a= ， b=；
（2）补全频数分布直方图；
（3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？
查看答案和解析>>
科目： 来源： 题型：
【题目】某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：
⑴若商店计划销售完这批商品后能获利1100元，问甲、乙两种商品应分别购进多少件?
⑵若商店计划投入资金少于4300元，且销售完这批商品后获利多于1260元，请问有哪几种购货方案?并求出最大获利。
甲 | 乙 | |
进价（元／件) | 15 | 35 |
售价（元／件) | 20 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
