
科目: 来源: 题型:
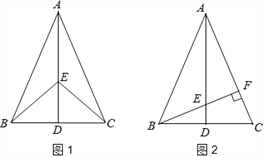
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l:y=x﹣ ![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y= ![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:;
(2)已知点Q是抛物线y= ![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.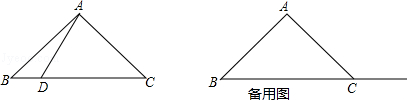
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB= ![]() ,则GE的长为
,则GE的长为 ![]() ,并简述求GE长的思路.
,并简述求GE长的思路.
查看答案和解析>>
科目: 来源: 题型:
【题目】将下列证明过程补充完整:
已知:如图,点B.E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知).
又因为∠1=∠ANC(______),
所以______(等量代换).
所以______∥______(同位角相等,两直线平行).
所以∠ABD=∠C(______).
又因为∠A=∠F(已知),
所以______∥______(______).
所以______(两直线平行,内错角相等).
所以∠C=∠D(______).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6). 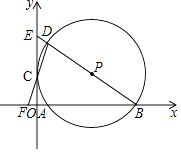
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com