（1）这两种台灯各购进多少盏？

（2）若A型台灯按标价的九折出售，B型台灯按标价的八折出售，那么这批台灯全部售完后，商场共获利多少元？

【题目】如图，对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B，与y轴交于点C，且点A的坐标为（﹣1，0）
注：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣ ， ）

（1）求抛物线的解析式；
（2）直接写出B、C两点的坐标；
（3）求过O，B，C三点的圆的面积．（结果用含π的代数式表示）

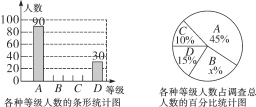
(1)求这次抽查的学生总数是多少人，并求出x的值；

(2)将不完整的条形统计图补充完整；

(3)若该校共有学生3600人，试估计每周课外阅读时间量满足2≤t〈4的人数.

（1）如图1，点E在直线BD的左侧，猜想∠ABE、∠CDE、∠BED的数量关系，并证明你的结论；

（2）如图2，点E在直线BD的左侧，BF、DF分别平分∠ABE、∠CDE，猜想∠BFD和∠BED的数量关系，并证明你的结论；

（3）如图3，点E在直线BD的右侧，BF、DF分别平分∠ABE、∠CDE；那么第（2）题中∠BFD和∠BED的数量关系的猜想是否仍成立？如果成立，请证明；如果不成立，请写出你的猜想，并证明．

(1)求yB关于x的函数解析式；

(2)如果A，B两种机器人连续搬运5小时，那么B种机器人比A种机器人多搬运了多少千克？

【题目】如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣4，0），C（0，0）

（1）画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；
（2）画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O；
（3）在x轴上存在一点P，满足点P到A1与点A2距离之和最小，请直接写出P点的坐标．

【题目】如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的 倍，得到矩形A1OC1B1 ， 再将矩形A1OC1B1以原点O为位似中心放大 倍，得到矩形A2OC2B2…，以此类推，得到的矩形AnOCnBn的对角线交点的坐标为 ．

解：∵AD∥BC，（　 　）

∴∠ACB+∠DAC=180° ，（　 　）

∵∠DAC=120°，（已知）

∴∠ACB=180°﹣∠DAC=　 　°.

∵∠ACF=20°（已知），

∴∠BCF=∠ACB﹣∠ACF=　 　°.

∵CE平分∠BCF，

∴∠BCE=∠BCF=　 　°.

∵EF∥AD，AD∥BC，

∴EF∥　 　 ，（　 　）

∴∠FEC=∠BCE=　 　°.（　 　）