
科目: 来源: 题型:
【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】填空完成推理过程:
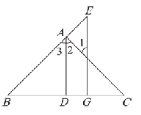
如图,AD⊥BC于点D,EG⊥BC于点G,AD平分∠BA C. 求证: ∠E=∠1.
证明: ∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,( )
∴∠1= ,( )
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,( )
∴∠E=∠1.(等量代换)
查看答案和解析>>
科目: 来源: 题型:
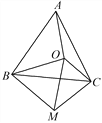
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点 B(m,n) 在第一象限,m,n 均为整数,且满足n =![]() .
.
(1) 求点 B 的坐标;
(2) 将线段 OB 向下平移 a 个单位后得到线段 O′B′,过点 B′作 B′C⊥y 轴于点 C,若 3CO=2CO′,求a 的值;
(3) 过点 B 作与 y 轴平行的直线 BM,点 D 在 x 轴上,点 E 在 BM 上,点 D 从 O 点出发以每秒钟 3个单位长度的速度沿 x 轴向右运动,同时点 E 从 B 点出发以每秒钟 2 个单位长度的速度沿BM 向下运动,在点 D,E 运动的过程中,若直线 OE,BD 相交于点 G,且 5≤S△OGB≤10,则点G 的横坐标 xG的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
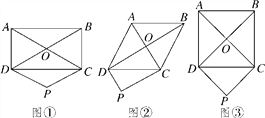
【题目】如图①,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP.
(1)判断四边形CODP的形状并说明理由;
(2)如图②,如果题目中的矩形变为菱形,判断四边形CODP的形状并说明理由;
(3)如图③,如果题目中的矩形变为正方形,判断四边形CODP的形状并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 ![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
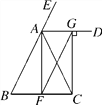
【题目】如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG;
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com