
科目: 来源: 题型:
【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)①若m=50,则射线OC的方向是________;
②图中与∠BOE互余的角有__________,与∠BOE互补的角有__________.
(2)若射线OA是∠BON的平分线,则∠BOS与∠AOC是否存在确定的数量关系?如果存在,请写出你的结论以及计算过程;如果不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O是边长为4 ![]() 的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= .
的等边△ABC的内心,将△OBC绕点O逆时针旋转30°得到△OB1C1 , B1C1交BC于点D,B1C1交AC于点E,则DE= . 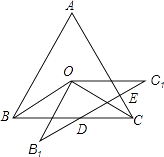
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

查看答案和解析>>
科目: 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com