
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( ) ①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.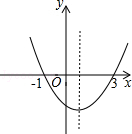
A.1
B.2
C.3
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧 ![]() 、
、 ![]() 是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )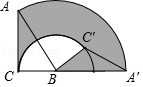
A.4π+2 ![]()
B.![]()
π﹣2 ![]()
C.![]()
π+2 ![]()
D.4π
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) 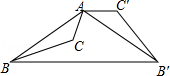
A.55°
B.65°
C.75°
D.85°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,O是AC上一动点(不与点A、C重合),过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)OE与OF相等吗?证明你的结论;
(2)试确定点O的位置,使四边形AECF是矩形,并加以证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).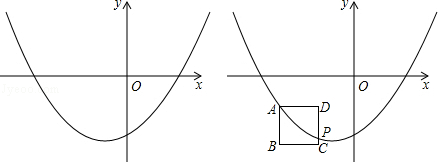
(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为;
(2)抛物线的对称轴为直线x=(用含b的代数式表示),位于y轴的
侧.
(3)思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y= ![]() (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(4)探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.
(1)发现:CD的最小值是 , 最大值是 , △CBD面积的最大值是 .
(2)思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长. 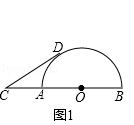
(3)探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
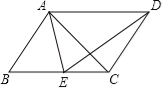
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.
查看答案和解析>>
科目: 来源: 题型:
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20 ![]() 米.
米.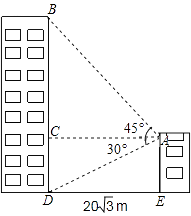
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com