（1）在直线l上共有多少射线？多少条线段？

（2）在直线l上增加一个点，共增加了多少条射线？多少条线段？

（3）如果在直线l上增加到n个点，则共有多少条射线？多少条线段？

【题目】如图，在直角坐标系中， B（0，8），D（10，0），一次函数y=x+的图象过C（16，n），与x轴交于A点。

（1）求证：四边形ABCD为平行四边形；

（2）将△AOB绕点O顺时针旋转，旋转得△A1OB1，问：能否使以点O、A1、D、B1为顶点的四边形是平行四边形？若能，求点A1的坐标；若不能，请说明理由；

(1)准确地画出图形，并标出相应的字母；

(2)线段DC的中点是哪个？线段AB的长是线段DC长的几分之几？

(3)求出线段BD的长度.

【题目】如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．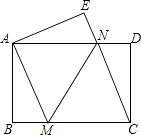
（1）求证：CM=CN；
（2）若△CMN的面积与△CDN的面积比为3：1，求 的值．

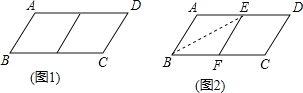
（1）判断与推理：

①邻边长分别为2和3的平行四边形是 阶准菱形；

②小明为了剪去一个菱形，进行如下操作：如图2，把□ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE．请证明四边形ABEF是菱形．

（2）操作、探究与计算：

①已知□ABCD是邻边长分别为1，a（a＞1），且是3阶准菱形，请画出□ABCD及裁剪线的示意图，并在图形下方写出a的值；

②已知□ABCD的邻边长分别为a，b（a＞b），满足a＝6b＋r，b＝5r（r＞0），则□ABCD

是 阶准菱形．

图1 图2

(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC=　　　　　　;

(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数.

【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况，随机抽取部分市民进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型，分别记为、、、.根据调查结果绘制了如下尚不完整的统计图.

（1）本次问卷共随机调查了 名市民，扇形统计图中 .

（2）请根据数据信息补全条形统计图.

（3）扇形统计图中“D类型”所对应的圆心角的度数是 .

（4）从这次接受调查的市民中随机抽查一个，恰好是“不了解”的概率是 。

【题目】如图,∠MON为锐角.下列说法:①∠MOP=∠MON;②∠MOP=∠NOP=∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( 　)

A. 1个 B. 2个 C. 3个 D. 4个

【题目】一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出一个球是红球的概率为 ．
（1）求口袋中黄球的个数；
（2）甲同学先随机摸出一个小球（不放回），再随机摸出一个小球，请用“树状图法”或“列表法”，求两次摸出都是红球的概率；
（3）现规定：摸到红球得5分，摸到黄球得3分，摸到蓝球得2分（每次摸后放回），乙同学在一次摸球游戏中，第一次随机摸到一个红球第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学三次摸球所得分数之和不低于10分的概率．

（1）该小区新建1个地上停车位和1个地下停车位各需多少万元？

（2）根据实际情况，该小区新建地上停车位不多于33个，且预计投资金额不超过11万元，共有几种建造方式？