
科目: 来源: 题型:
【题目】阅读理解:
(1)如图(1),等边△ABC内有一点P到顶点A,B,C的距离分别为3,4,5,则∠APB= .
分析:由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌ , 这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:BE2+CF2=EF2 .
查看答案和解析>>
科目: 来源: 题型:
【题目】为推广阳光体育“大课间”活动,某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目,为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: 
(1)在这项调查中,共调查了多少名学生?
(2)请计算喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的4名学生中有2名男生,2名女生.现从这4名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目: 来源: 题型:
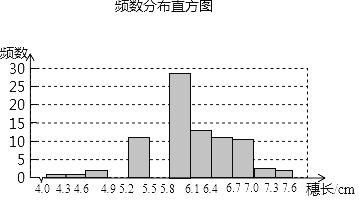
【题目】为了考察某种大麦细长的分布情况,在一块试验田里抽取了部分麦穗.测得它们的长度,数据整理后的频数分布表及频数分直方图如下.根据以下信息,解答下列问题:
穗长x | 频数 |
4.0≤x<4.3 | 1 |
4.3≤x<4.6 | 1 |
4.6≤x<4.9 | 2 |
4.9≤x<5.2 | 5 |
5.2≤x<5.5 | 11 |
5.5≤x<5.8 | 15 |
5.8≤x<6.1 | 28 |
6.1≤x<6.4 | 13 |
6.4≤x<6.7 | 11 |
6.7≤x<7.0 | 10 |
7.0≤x<7.3 | 2 |
7.3≤x<7.6 | 1 |
(Ⅰ)补全直方图;
(Ⅱ)共抽取了麦穗 棵;
(Ⅲ)频数分布表的组距是 ,组数是 ;
(Ⅳ)麦穗长度在5.8≤x<6.1范围内麦穗有多少棵?占抽取麦穗的百分之几?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(﹣1,2),B(﹣2,0),C(﹣4,1),把三角形ABC向上平移1个单位长度,向右平移5个单位长度,可以得到三角形A′B′C′.
(Ⅰ)在图中画出△A′B′C′;
(Ⅱ)直接写出点A′、B′、C′的坐标;
(Ⅲ)写出A′C′与AC之间的位置关系和大小关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】因市场竞争激烈,国商进行促销活动,决定对学习用品进行打八折出售,打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元.
(1)求打折前1本笔记本,1支圆珠笔各需要多少元.
(2)在促销活动时间内,购买50本笔记本和40支圆珠笔共需要多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是一个新款水杯,水杯不盛水时按如图2所示的位置放置,这样可以快速晾干杯底,干净透气;将图2的主体部分的抽象成图3,此时杯口与水平直线的夹角35°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F. 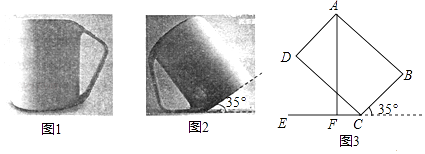
(1)求∠BAF的度数;(sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
(2)求点A到水平直线CE的距离AF的长(精确到0.1cm)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是 ![]() 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( ) 
A.15°
B.20°
C.25°
D.30°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AC、AB的中点,连DE、CE.则下列结论中不一定正确的是( ) 
A.ED∥BC
B.ED⊥AC
C.∠ACE=∠BCE
D.AE=CE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com