【题目】为了了解某市初中学生上学的交通方式，从中随机调查了a名学生的上学交通方式，统计结果如图．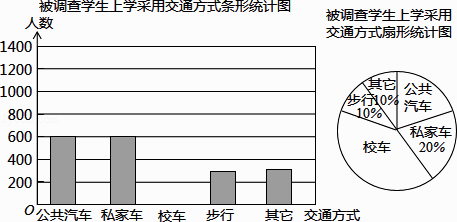
（1）求a的值；
（2）补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数；
（3）该市共有初中学生15000名，请估计其中坐校车上学的人数．

【题目】如图，小明想测山高度，他在B处仰望山顶A，测得仰角∠B=31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=39°．求这座山的高度（小明的身高忽略不计）．
【参考数据：tan31°≈ ，sin31°≈ ，tan39°≈ ，sin39°≈ 】

【题目】如果点将线段分成两条相等的线段和，那么叫做线段的二等分点(中点);如果点，将线段分成三条相等的线段，和，那么，叫做线段的三等分点;…;依此类推，如果点将线段分成条相等的线段，那么叫做线段的等分点，如图①所示.

已知点在直线的同侧，请回答下列问题.

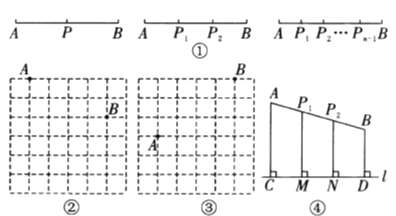
(1)在所给边长为个单位长度的正方形网格中，探究:

①如图②，若点到直线的距离分别是4个单位长度和2个单位长度，则线段 的中点到直线的距离是 个单位长度;

②如图③，若点到直线的距离分别是2个单位长度和5个单位长度，则线段 的中点到直线的距离是 个单位长度;

③由①②可以发现结论:若点到直线的距离分别是个单位长度和个单位长度，则线段 的中点到直线的距离是 个单位长度.

(2)如图④，若点到直线的距离分别是和，利用(1)中的结论求线段的三等分点，到直线的距离分别是 .

(3)若点到直线的距离分别是和，点为线段的等分点，直接写出第个等分点到直线的距离.

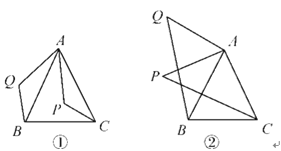
“如图①，已知，在△ABC中，AB＝AC，P是△ABC内任意一点，将AP绕点A顺时针旋转至AQ，使∠QAP＝∠BAC，连接BQ，CP，则BQ＝CP.”

小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ＝CP之后，他将点P移到等腰三角形ABC外，原题中其他条件不变，发现“BQ＝CP”仍然成立，请你就图②给出证明．

【题目】将5个完全相同的小球分装在甲、乙两个不透明的口袋中．甲袋中有3个球，分别标有数字2，3，4；乙袋中有2个球，分别标有数字2，4．从甲、乙两个口袋中各随机摸出一个球．
（1）用列表法或画树状图法，求摸出的两个球上数字之和为5的概率．
（2）摸出的两个球上数字之和为多少时的概率最大？

【题目】若一次函数y=kx+b的图象如图所示，则k，b的值可能为（ ）

A.k=3，b=3
B.k=3，b=﹣3
C.k=﹣3，b=3
D.k=﹣3，b=﹣3

我们知道:一条线段有两个端点，线段和线段表示同一条线段. 若在直线上取了三个不同的点，则以它们为端点的线段共有 条;若取了四个不同的点，则共有线段 条;…;依此类推，取了个不同的点，共有线段条.(用含的代数式表示)

类比探究:

以一个锐角的顶点为端点向这个角的内部引射线.

(1)若引出两条射线，则所得图形中共有 个锐角;

(2)若引出条射线，则所得图形中共有 个锐角.(用含的代数式表示)

拓展应用:

一条铁路上共有8个火车站，若一列火车往返过程中必须停靠每个车站，则铁路局需为这条线路准备多少种车票?

(1)如图①，若点O在边BC上，求证：AB＝AC；

(2)如图②，若点O在△ABC的内部，求证：AB＝AC；

(3)若点O在△ABC的外部，AB＝AC成立吗？请画图表示．

【题目】如图，是直线上的一点，是任意一条射线，平分，平分.

(1)图中的补角为 ;

(2)若，求的度数;

(3)与存在怎样的数量关系?

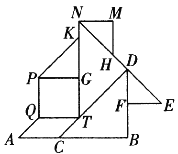
(1)请赋予该图形一个积极的含义;

(2)请你找出图中2组平行线段和2对互相垂直的线段，用符号表示它们;

(3)找出图中一个锐角、一个钝角和一个直角，将它们表示出来，并指出它们的度数.