（1）求该什锦糖的单价．
（2）为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中加入甲、丙两种糖果共100千克，问其中最多可加入丙种糖果多少千克？

（1）画出格点△ABC关于直线DE的对称的△A1B1C1；

（2）在DE上画出点P，使PA+PC最小；

（3）在DE上画出点Q，使QA﹣QB最大．

【题目】如图，直线l1过点A（0，4），点D（4，0），直线l2：与x轴交于点C，两直线，相交于点B．

（1）求直线的解析式和点B的坐标；

（2）求△ABC的面积．

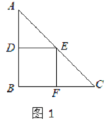
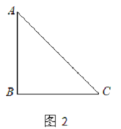
（1）要在这张纸板上剪出一个正方形，使这个正方形的四个顶点都在△ABC的边上．小林设计出了一种剪法，如图1所示．请你再设计出一种不同于图1的剪法，并在图2中画出来．

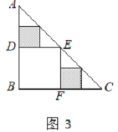
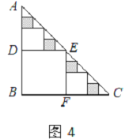
（2）若按照小林设计的图1所示的剪法来进行裁剪，记图1为第一次裁剪，得到1个正方形，将它的面积记为，则=___________；在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪（如图3），得到2个新的正方形，将此次所得2个正方形的面积的和记为，则=___________；在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪（如图4），得到4个新的正方形，将此次所得4个正方形的面积的和记为；按照同样的方法继续操作下去……，第次裁剪得到_________个新的正方形，它们的面积的和=______________．

【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”，但是在实际丈量土地面积时，量出高并非易事，所以古人想到了能否利用三角形的三条边长来求面积．我国南宋著名的数学家秦九韶（年—年）提出了“三斜求积术”，阐述了利用三角形三边长求三角形面积方法，简称秦九韶公式．在海伦（公元年左右，生平不详）的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法，相传这个公式最早是由古希腊数学家阿基米德（公元前年—公元前年）得出的，故我国称这个公式为海伦一秦九韶公式．它的表达为：三角形三边长分别为、、，则三角形的面积（公式里的为半周长即周长的一半）．

请利用海伦一秦九韶公式解决以下问题：

（）三边长分别为、、的三角形面积为__________．

（）四边形中，，，，，，四边形的面积为__________．

（）五边形中，，，，，，，五边形的面积为__________．

【题目】如图，已知∠ACB=∠DCE=90°，AC=BC，AB=，CE=CD，AE=2，∠CAE=45°，求AD的长．

（1）此次共调查了　 　名学生；

（2）将条形统计图补充完整；

（3）图2中“小说类”所在扇形的圆心角为　 　度；

（4）若该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数．

【题目】如图，已知一次函数的图象与x轴、y轴分别交于A、B两点且与反比例函数的图象在第一象限交于C点，CD⊥轴于D点，若∠CAD=，AB =，CD =

（1）求点A、B、D的坐标；

（2）求一次函数的解析式；

（3）反比例函数的解析式；

（4）求△BCD的面积.