
科目: 来源: 题型:
【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题 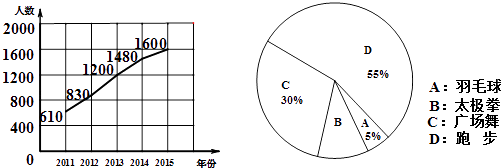
(1)2015年比2011年增加人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为 ![]() 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
的等腰直角三角形DEF的费马点,则PD+PE+PF= .
查看答案和解析>>
科目: 来源: 题型:
【题目】定义,我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE.若AC=2,AB=5,则①求证:△AGB≌△ACE;
②GE= .

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,Rt△ABC中,∠C=90°,BC=6,AC=8.动点P从点A出发沿A—B—C的方向以每秒2个单位的速度运动.设P的运动时间为t(秒).
(1)请直接用含t的代数式表示①当点P在AB上时,BP= ;②当点P在BC上时,BP= ;
(2)求△BPC为等腰三角形的t值.

 (备用图)
(备用图)
查看答案和解析>>
科目: 来源: 题型:
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭轿车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成不完整的条形统计图(图1)和扇形统计图(图2),请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民;
(2)扇形统计图中,C组的百分率是 ;并补全条形统计图;
(3)计算四市中10000名市民上班时最常用家庭轿车的有多少?


查看答案和解析>>
科目: 来源: 题型:
【题目】已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1 , 直线CD的表达式为y2=k2x+b2 , 则k1k2= . 
查看答案和解析>>
科目: 来源: 题型:
【题目】长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD+PE的和最小,则这个和的最小值是( ).

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com