
科目: 来源: 题型:
【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.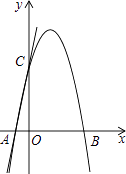
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1 , y1),Q(x2 , y2),
当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1﹣x2|求出;
当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1﹣y2|求出.
查看答案和解析>>
科目: 来源: 题型:
【题目】解答
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:① EF=BE+CF;②∠BGC=90°+![]() ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则![]() =mn. 其中正确的结论有( )
=mn. 其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8. 
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E,求由线段ED,BE, ![]() 所围成区域的面积.(其中
所围成区域的面积.(其中 ![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
(1)问线段EC与BF数量关系和位置关系?并给予证明.
(2)连AM,请问∠AME的大小是多少,如能求写出过程;不能求,写出理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= ![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2). 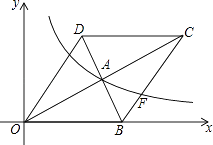
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目: 来源: 题型:
【题目】“蘑菇石”是我省著名自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1790m.如图,DE∥BC,BD=1700m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m) 
查看答案和解析>>
科目: 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com