
科目: 来源: 题型:
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An﹣1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y= ![]() (x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2017= .
(x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2017= . 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1 , 当点C1、B1、C三点共线时,旋转角为α,连接BB1 , 交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1 , 其中正确的是( ) 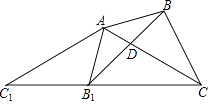
A.①③④
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y= ![]() x2+bx﹣
x2+bx﹣ ![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知双曲线y= ![]() (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ![]() ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y= ![]() (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是多少?
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y= ![]() 与y轴交于点A,与直线y=﹣
与y轴交于点A,与直线y=﹣ ![]() 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣ ![]() 上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2 ![]()
B.﹣2≤h≤1
C.﹣1 ![]()
D.﹣1 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com