【题目】已知抛物线E1：y=x2经过点A（1，m），以原点为顶点的抛物线E2经过点B（2，2），点A、B关于y 轴的对称点分别为点A′，B′．

（1）求m的值及抛物线E2所表示的二次函数的表达式;
（2）如图1，在第一象限内，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由;
（3）如图2，P为第一象限内的抛物线E1上与点A不重合的一点，连接OP并延长与抛物线E2相交于点P′，求△PAA′与△P′BB′的面积之比．

【题目】已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1 ， BP绕点B顺时针也旋转角α得到BP2 ， 连接PP1、PP2 ．

（1）如图1，当α=90°时，求∠P1PP2的度数;
（2）如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA;
（3）如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2 ， l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．

【题目】大学生小刘回乡创办小微企业，初期购得原材料若干吨，每天生产相同件数的某种产品，单件产品所耗费的原材料相同．当生产6天后剩余原材料36吨，当生产10天后剩余原材料30吨．若剩余原材料数量小于或等于3吨，则需补充原材料以保证正常生产．
（1）求初期购得的原材料吨数与每天所耗费的原材料吨数;
（2）若生产16天后，根据市场需求每天产量提高20%，则最多再生产多少天后必须补充原材料？

【题目】如图，在ABCD中，对角线AC与BD相交于点O，∠CAB=∠ACB，过点B作BE⊥AB交AC于点E．

（1）求证：AC⊥BD;
（2）若AB=14，cos∠CAB=，求线段OE的长．

【题目】2014年益阳市的地区生产总值（第一、二、三产业的增加值之和）已进入千亿元俱乐部，如图表示2014年益阳市第一、二、三产业增加值的部分情况，请根据图中提供的信息解答下列问题

（1）2014年益阳市的地区生产总值为多少亿元？
（2）请将条形统计图中第二产业部分补充完整;
（3）求扇形统计图中第二产业对应的扇形的圆心角度数．

【题目】如图，直线l上有一点P1（2，1），将点P1先向右平移1个单位，再向上平移2个单位得到像点P2 ， 点P2恰好在直线l上．

（1）写出点P2的坐标;
（2）求直线l所表示的一次函数的表达式;
（3）若将点P2先向右平移3个单位，再向上平移6个单位得到像点P3 ． 请判断点P3是否在直线l上，并说明理由．

【题目】如图，二次函数y=ax2+2x+c的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．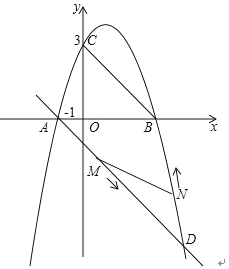

（1）求该二次函数的表达式;
（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式;
（3）在（2）的条件下，请解答下列问题：
①在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由；
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动，同时，动点N以每秒个单位的速度沿线段DB从点D向点B运动，问：在运动过程中，当运动时间t为何值时，△DMN的面积最大，并求出这个最大值．

【题目】如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．

（1）求证：△AEH≌△CGF
（2）求证：四边形EFGH是菱形．

【题目】阅读下列材料，并解决相关的问题．
按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为a1 ， 依此类推，排在第n位的数称为第n项，记为an ．
一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q表示（q≠0）．如：数列1，3，9，27，…为等比数列，其中a1=1，公比为q=3．
（1）等比数列3，6，12，…的公比q为 ，第4项是
（2）如果一个数列a1 ， a2 ， a3 ， a4 ， …是等比数列，且公比为q，那么根据定义可得到：=q，=q，=q，…=q．
所以：a2=a1q，a3=a2q=（a1q）q=a1q2 ， a4=a3q=（a1q2）q=a1q3 ， …
由此可得：an=（用a1和q的代数式表示）．
（3）若一等比数列的公比q=2，第2项是10，请求它的第1项与第4项．

【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．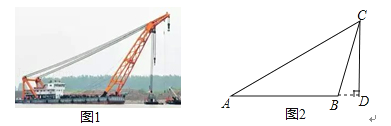

（1）求点B到AC的距离.
（2）求线段CD的长度．