
科目: 来源: 题型:
【题目】解答题
(1)如图1,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,连结BE,CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,求BD的长.
(3)如图3,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα= ![]() ,CD=5,AD=12,求BD的长.
,CD=5,AD=12,求BD的长.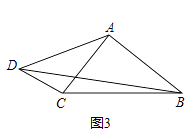
查看答案和解析>>
科目: 来源: 题型:
【题目】如今,网上购物已成为一种新的消费时尚,精品书店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网
店(如图所示),已知两家网店的这种贺年卡的质量相同,请看图回答下列问题:
(1)假若精品书店想购买x张贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含有x的式子表示)?(提示:如需付运费时运费只需付一次,即8元)
(2)精品书店打算购买300张贺年卡,选择哪家网店更省钱?

查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)若该抛物线经过原点O,且a=﹣ ![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在(1)的条件下,点P(m,n)在抛物线上,且∠POB锐角,满足∠POB+∠BCD<90°,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEO的度数是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC. 
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a= , b=;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com