
科目: 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )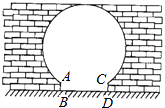
A.2米
B.2.5米
C.2.4米
D.2.1米
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.直线PE从B点出发,以2cm/s的速度向点A方向运动,并始终与BC平行,与AC交于点E.同时,点F从C点出发,以1cm/s的速度沿CB向点B运动,设运动时间为t (s)(0<t<5).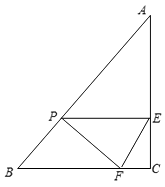
(1)当t为何值时,四边形PFCE是矩形?
(2)设△PEF的面积为S(cm2),求S与t的函数关系式;
(3)是否存在某一时刻t,使△PEF的面积是△ABC面积的 ![]() ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接BE,是否存在某一时刻t,使PF经过BE的中点?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车,已知过去租用这两种汽车运货的情况如下表所示.
甲货车辆数 | 乙货车辆数 | 累计运货吨数 | |
第一次 | 3 | 4 | 54 |
第二次 | 2 | 3 | 39 |
(1)一辆甲货车和一辆乙货车一次分别运货多少吨?
(2)若货主现有45吨货物,计划同时租用甲货车a辆,乙货车b辆,一次运完,且恰好每辆车都装满货物.
①请你帮助货主设计租车方案;
②若甲货车每辆租金200元,乙货车每辆租金240元.请选出省钱的租车方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.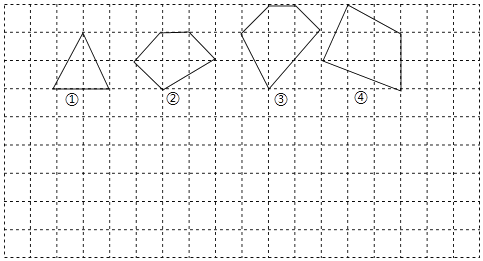
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).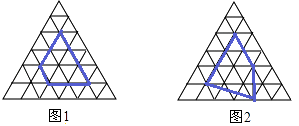
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用 ![]() 刻画.
刻画.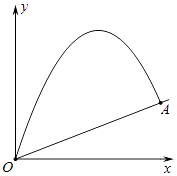
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.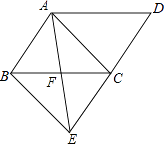
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(-3,4).
(1)求AO的长;
(2)求直线AC的解析式和点M的坐标;
(3)如图2,点P从点A出发,以每秒2个单位的速度沿折线A-B-C运动,到达点C终止.设点P的运动时间为t秒,△PMB的面积为S.
①求S与t的函数关系式;
②求S的最大值.
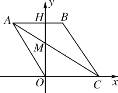
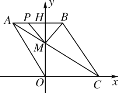
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com