
科目: 来源: 题型:
【题目】下图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )
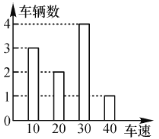
A. 平均数是23 B. 中位数是25 C. 众数是30 D. 方差是129
查看答案和解析>>
科目: 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A(____,___),B(______,_______),C(______,_______);
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2(_____,____)B2(____,____)(其中A2与A对应,B2与B对应,不必画图.)
查看答案和解析>>
科目: 来源: 题型:
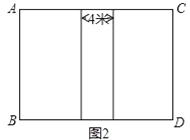
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( ) 
A.∠1=∠2
B.BE=DF
C.∠EDF=60°
D.AB=AF
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为( )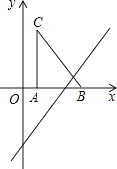
A.4
B.8
C.16
D.8 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A | B | C | D | E | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.
查看答案和解析>>
科目: 来源: 题型:
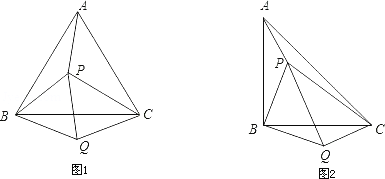
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<0),过点P作PD⊥BC于点D.
①求线段PD的长的最大值;②当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com