
科目: 来源: 题型:
【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.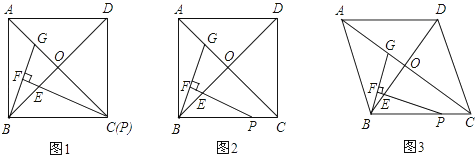
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: ![]() 与
与 ![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.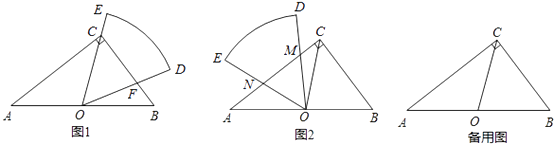
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣ ![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2 , 求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
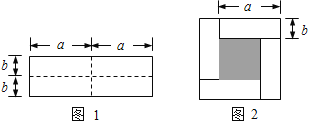
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目: 来源: 题型:
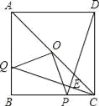
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() .
.
(1)如下图,点![]() 在直线
在直线![]() 的左侧,请写出
的左侧,请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由:
之间的数量关系,并说明理由:
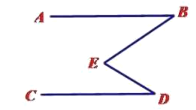
(2)如下图,当点![]() 在线段
在线段![]() 上时,
上时,![]() 分别平分
分别平分![]() ,
,![]() ,此时
,此时![]() 的度数为_________°
的度数为_________°
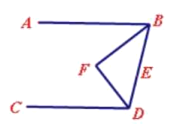
(3)如下图,当点![]() 在直线
在直线![]() 的左侧时,
的左侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
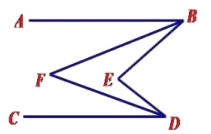
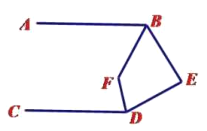
(4)如下图,当点![]() 在直线
在直线![]() 的右侧时,
的右侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com