
科目: 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】把抛物线y=﹣ ![]() 经( )平移得到y=﹣
经( )平移得到y=﹣ ![]() ﹣1.
﹣1.
A.向右平移2个单位,向上平移1个单位
B.向右平移2个单位,向下平移1个单位
C.向左平移2个单位,向上平移1个单位
D.向左平移2个单位,向下平移1个单位
查看答案和解析>>
科目: 来源: 题型:
【题目】四川雅安地震牵动全国人民的心,同学们都在积极进行捐款活动.某校九(2)班同学人人拿出自己的零花钱,踊跃募捐,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.则该班同学平均捐款 ( )
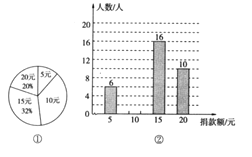
A. 12元 B. 12.5元 C. 13元 D. 13.5元
查看答案和解析>>
科目: 来源: 题型:
【题目】快递公司准备购买机器人来代替人工分拣已知购买- 台甲型机器人比购买-台乙型机器人多![]() 万元;购买
万元;购买![]() 台甲型机器人和
台甲型机器人和![]() 台乙型机器人共需
台乙型机器人共需![]() 万元.
万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型、乙型机器人每台每小时分拣快递分别是![]() 件、
件、![]() 件,该公司计划最多用
件,该公司计划最多用![]() 万元购买
万元购买![]() 台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、6,则四边形DHOG的面积是( )
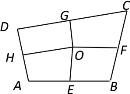
A. 5B. 4C. 8D. 6
查看答案和解析>>
科目: 来源: 题型:
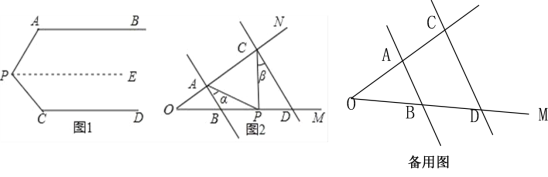
【题目】问题情境:如图1,AB∥CD,∠PAB=125°,∠PCD=135°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度。
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,①如果点P运动到D点右侧(不包括D点),则∠APC与α、β之间的数量关系为 .②如果点P运动到B点左侧(不包括B点),则∠APC与α、β之间的数量关系 .(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边三角形ABC中,AD=BE=CF,D、E、F不是各边的中点,AE、BF、CD分别交于P、M、H,如果把三个三角形全等叫做一组全等三角形,那么图中全等三角形有( )
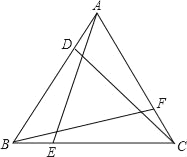
A. 6组 B. 5组 C. 4组 D. 3组
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上
(1)求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;
(2)当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;
(3)抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com