
科目: 来源: 题型:
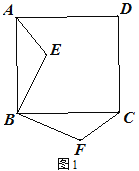
【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①![]() ;②
;②![]() .
.
(2)若![]() ,
,
① 如图2,点E在正方形内,连接EC,若![]() ,
, ![]() ,求
,求![]() 的长;
的长;
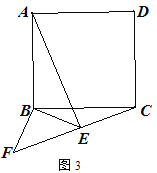
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的方格形中,点A、B、C在小正方形的顶点上.在BC上找一点P,使点P到AB和AC的距离相等.
实验与操作:
(1)在BC上找一点P,使点P到AB和AC的距离相等;
(2)在射线AP上找到一点Q,使QB=QC.
探索与计算:
如果A点坐标为(-1,-3),
(1)试在图中建立平面直角坐标系;
(2)若点M、N是坐标系中小正方形的顶点,且四边形QCMN是一个正方形,则 M点的坐标是__________,N点的坐标是___________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)△BEF是等腰三角形吗?试说明理由;
(2)若AB=4,AD=8,求CF的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A、B的坐标分别为A(-4,0)、B(2,0),点C在y轴上,且△ABC的面积为6,以点A、B、C为顶点作□ABCD.若过原点的直线平分该□ABCD的面积,则此直线的解析式是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】设A1,A2,A3,A4是数轴上的四个不同点,若|A1A3|=λ|A1A2|,|A1A4|=η|A1A2|,且![]() ,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
A. 点C可能是线段AB的中点
B. 点C,D可能同时在线段AB上
C. 点D一定不是线段AB的中点
D. 点C,D可能同时在线段AB的延长线上
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列各式:定义一种新运算“⊙”:
1⊙3=1×4+3=7,3⊙﹣1=3×4﹣1=11,5⊙4=5×4+4=24
4⊙(﹣3)=4×4﹣3=13,(﹣2)⊙(﹣5)=(﹣2)×4﹣5=﹣13,……
(1)写出一般结论:a⊙b=_____;
(2)如果a≠b,那么a⊙b_____b⊙a(填“=”或“≠”)
(3)先化简,再求值:(a﹣b)⊙(2a+3b).其中a=﹣![]() ,b=2019.
,b=2019.
查看答案和解析>>
科目: 来源: 题型:
【题目】丁丁想在一个矩形材料中剪出如图阴影所示的梯形,作为要制作的风筝的一个翅膀.请你根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位, ![]() ≈1.7).
≈1.7). 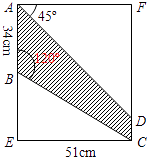
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com