【题目】如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．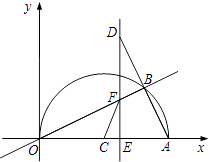
（1）当∠AOB=30°时，求弧AB的长度；
（2）当DE=8时，求线段EF的长；
（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．

（1）t= min.

（2）若乙提速后，乙登山的上升速度是甲登山的上升速度3倍，

①则甲登山的的上升速度是 m/min；

②请求出甲登山过程中，距地面的高度y(m)与登山时间x(min)之间的函数关系式.

③当甲、乙两人距地面高度差为70m时，求x的值（直接写出满足条件的x值）.

【题目】如图，点A（1，3）、点B（m，1）是一次函数的图像上的两点，一次函数图像与x轴交于点D.

（1）b = ，m = ；

（2）过点B作直线l垂直于x轴，点E是点D关于直线l的对称点，点C是点A关于原点的对称点．试判断点B、E、C是否在同一条直线上，并说明理由．

（3）连结AO、BO，求△AOB的面积；

【题目】在平面直角坐标系中，如图1，将n个边长为1的正方形并排组成矩形OABC，相邻两边OA和OC分别落在x轴和y轴的正半轴上，设抛物线y=ax2+bx+c（a＜0）过矩形顶点B、C．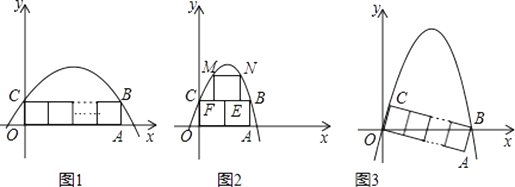
（1）当n=1时，如果a=﹣1，试求b的值；
（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；
（3）将矩形OABC绕点O顺时针旋转，使得点B落到x轴的正半轴上，如果该抛物线同时经过原点O． ①试求当n=3时a的值；
②直接写出a关于n的关系式．

【题目】解方程： （1）x﹣3＝-2x+1 （2）18（x-1）＝-2（2x﹣1）（3）

（1）﹣ ﹣[(﹣3) ﹣2× ﹣8.5]÷(﹣ )

（2）× ﹣0.25×（﹣4）×(﹣3)；

（3）（﹣1）﹣1+（﹣ ）﹣3﹣（﹣1）

（4）÷4 ×(﹣)+5﹣2×（﹣ ）

【题目】某班师生组织植树活动，上午8时从学校出发，到植树地点植树后原路返校，如图为师生离校路程s与时间t之间的图象．请回答下列问题：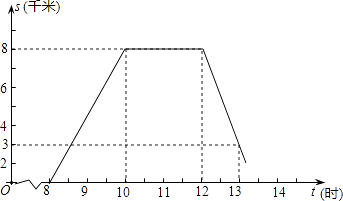
（1）求师生何时回到学校？
（2）如果运送树苗的三轮车比师生迟半小时出发，与师生同路匀速前进，早半小时到达植树地点，请在图中，画出该三轮车运送树苗时，离校路程s与时间t之间的图象，并结合图象直接写出三轮车追上师生时，离学校的路程；
（3）如果师生骑自行车上午8时出发，到植树地点后，植树需2小时，要求14时前返回到学校，往返平均速度分别为每时10km、8km．现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km，试通过计算说明哪几个植树点符合要求．

【题目】如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．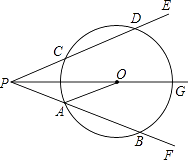
（1）求证：AP=AO；
（2）若tan∠OPB= ，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ， 能构成等腰梯形的四个点为或或 ．

【题目】王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示．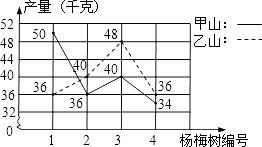
（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；
（2）试通过计算说明，哪个山上的杨梅产量较稳定？

AE⊥BC于点E，EF⊥AD于点F.

(1)求∠DAC的度数；

(2)求∠DEF的度数．