问题：(1)这种解方程组的方法叫什么方法；嘉嘉的解法正确吗？如果不正确，从哪一步开始出错的？请你指出错误的原因，并求出正确的解．

(2)请用不同于(1)中的方法解这个方程组．

【题目】若抛物线y=x2﹣2x+c与y轴的交点为（0，﹣3），则下列说法不正确的是（ ）
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时，y的最大值为﹣4
D.抛物线与x轴的交点为（﹣1，0），（3，0）

【题目】如图，在ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（ ）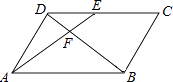
A.2：5
B.2：3
C.3：5
D.3：2

证明过程如下：

证明：过点E作EF∥AB，

∵AB∥DC，EF∥AB（辅助线的作法），

∴EF∥DC

∴∠C=∠CEF．

∵EF∥AB，∴∠B=∠BEF

∴∠B+∠C=∠CEF+∠BEF

即∠B+∠C=∠BEC．

（2）如果点E运动到图②所示的位置，其他条件不变，∠B，∠C，∠BEC又有什么关系？并证明你的结论；

（3）如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A=　　　　　　．（写出结论，不用写计算过程）。

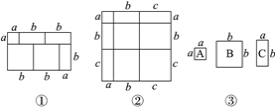
(1)由图②，写出所得的等式；

(2)利用(1)中所得到的结论，解决下面的问题： 已知a＋b＋c＝11，ab＋bc＋ac＝38，求a2＋b2＋c2的值；

(3)如图③，琪琪用2 张A型纸片，3 张B型纸片，5 张C型纸片拼出一个长方形，那么该长方形较长的一条边长为多少．(直接写出答案)

(1)甲、乙两组工作一天，商店各应付多少钱？

(2)已知甲组单独完成需12天，乙组单独完成需24天，单独请哪个组，商店所需费用

较少？

(3)若装修完后，商店每天可赢利200元，现有三种方案：①甲组单独做；②乙组单独做；③甲、乙两组同时做．你认为哪一种施工方案更有利于商店？请你帮商店做出决策(可用(1)(2)问中的条件及结论)．

【题目】阅读下面计算+++…+的过程，然后填空．

解：∵=（-），=（-），…，=（-），

∴+++…+

=（-）+（-）+（-）+…+（-）

=（-+-+-+…+-）

=（-）

=．

以上方法为裂项求和法，请参考以上做法完成：

（1）+=______；

（2）当+++…+x=时，最后一项x=______．

【题目】如图，抛物线y1=x2﹣1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2 ， 两条抛物线相交于点C．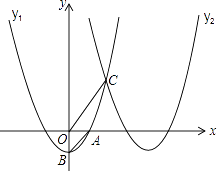

（1）请直接写出抛物线y2的解析式；
（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；
（3）在第四象限内抛物线y2上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q的坐标及h的最大值；若不存在，请说明理由．

证明：∵DG⊥BC，AC⊥BC（已知）

∴∠DGB=∠ACB=90°（垂直定义）

∴DG∥AC（ ）

∴∠2= （ ）

∵∠1=∠2（已知）

∴∠1=∠ （等量代换）

∴EF∥CD（ ）

∴∠AEF=∠ （ ）

∵EF⊥AB（已知）

∴∠AEF=90°（ ）

∴∠ADC=90°（ ）

∴CD⊥AB（ ）

9：00时看到的两位数是（　　）

A. 54 B. 45 C. 36 D. 27