【题目】
（1）计算（2017﹣π）0﹣（ ）﹣1+|﹣2|
（2）化简（1﹣ ）÷（ ）．

【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．则下列说法正确的是 ． （写出所有正确说法的序号） ①当x=1.7时，[x]+（x）+[x）=6；
②当x=﹣2.1时，[x]+（x）+[x）=﹣7；
③方程4[x]+3（x）+[x）=11的解为1＜x＜1.5；
④当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有两个交点．

（1）AC= cm，BC= cm；

（2）当t为何值时，AP=PQ；

（3）当t为何值时，P与Q第一次相遇；

（4）当t为何值时，PQ=1cm．

材料：将分式拆分成一个整式与一个分式（分子为整数）的和的形式．

解：由分母为﹣x2+1，可设﹣x4﹣x2+3=（﹣x2+1）（x2+a）+b则﹣x4﹣x2+3=（﹣x2+1）（x2+a）+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣（a﹣1）x2+（a+b）

∵对应任意x，上述等式均成立，∴，∴a=2，b=1

∴==+=x2+2+这样，分式被拆分成了一个整式x2+2与一个分式的和．

解答：

（1）将分式 拆分成一个整式与一个分式（分子为整数）的和的形式．

（2）试说明的最小值为8．

（1﹣）=（1﹣）（1+）

（1﹣）=（1﹣）（1+）

（1﹣）=（1﹣）（1+）

观察上面的算式，可以归纳得出： =　 　．

利用上述规律，计算下列各式：（1﹣）×（1﹣）×（1﹣）=　 　．

（1﹣）×（1﹣）×（1﹣）×…×（1﹣）=　 　（请将结题步骤写在下方空白处）

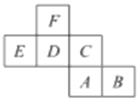
【题目】如图是一个正方体的展开图，标注了字母，的面分别是正方体的正面和底面，其他面分别用字母，，，表示．已知，，，，，．

(1)如果正方体的左面与右面所标注字母代表的代数式的值相等，求出的值；

(2)如果正面字母代表的代数式与对面字母代表的代数式的值相等，且为整数，求整数的值．

【题目】如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G，AE=2，则EG的长是 ．

A超市：购物金额打9折后，若超过2000元再优惠300元；

B超市：购物金额打8折．

某学校计划购买某品牌的篮球做奖品，该品牌的篮球在A，B两个超市的标价相同．根据商场的活动方式：

（1）若一次性付款4200元购买这种篮球，则在B商场购买的数量比在A商场购买的数量多5个．请求出这种篮球的标价；

（2）学校计划购买100个篮球，请你设计一个购买方案，使所需的费用最少．（直接写出方案）

(1)小林家在4月份用电度，请你用来表示小林家在4月份应付的电费：_________；

(2)小林家在12月份交付电费181元，请你利用方程的知识，求小林家在12月份的用电量．