
科目: 来源: 题型:
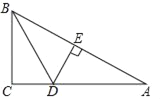
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,DE垂直平分AB,垂足为E,若BC=3,则AD的长为( )
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 4
D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料并解答下列问题.
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.

查看答案和解析>>
科目: 来源: 题型:
【题目】作图题:如图,在平面直角坐标系 xOy 中,A(2,3),B(3,1),C(﹣2,﹣1).
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1,B1,C1 的坐标;
②在 y 轴上画出点 P,使 PA+PB 最小.(不写作法,保留作图痕迹)
③求△ABC 的面积.

查看答案和解析>>
科目: 来源: 题型:
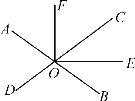
【题目】如图,直线AB,CD相交于点O,OE是∠COB的平分线,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度数;
(2)OF是∠AOC的平分线吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= ![]() ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 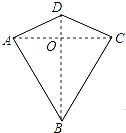
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于 ![]() BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )
BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( ) 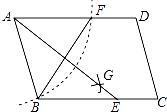
A.11
B.6
C.8
D.10
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com