
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表: 
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】用不等式表示下列关系:
(1)m与10的和不小于m的一半:________;
(2)3与x的5倍的差是非负数:________;
(3)长为a,宽为a-1的长方形的面积小于边长为a的正方形的面积:________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( ) 
A.( ![]() )2016倍
)2016倍
B.( ![]() )2017倍
)2017倍
C.( ![]() )2018倍
)2018倍
D.( ![]() )2019倍
)2019倍
查看答案和解析>>
科目: 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
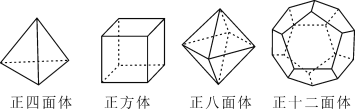
(1)根据上面的多面体模型,完成表格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
正方体 | 8 | 12 | |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
查看答案和解析>>
科目: 来源: 题型:
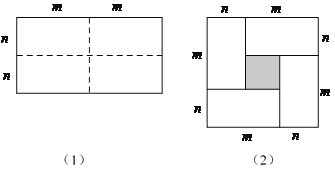
【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:![]() ,
,![]() ,
,![]() ;
;
(3)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y= ![]() 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2<
在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2< ![]() 的解集是0<x<1.其中正确的有( )
的解集是0<x<1.其中正确的有( ) 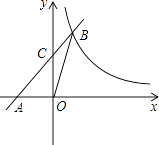
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 ![]() m,弦CD=4m,那么隧道的最高处到CD的距离是( )
m,弦CD=4m,那么隧道的最高处到CD的距离是( ) 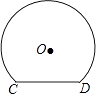
A.![]() m
m
B.4m
C.![]() m
m
D.6m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com