
科目: 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究: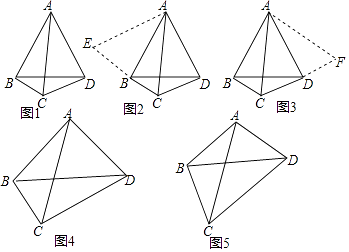
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,D为AB中点,点E,F分别在AC,BC边上,且AE=CF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
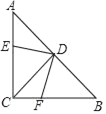
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,已点A(3,0)、B(-5,3),将点A向左平移6个单位到达C点,将点B向下平移6个单位到达D点.
(1)写出C点、D点的坐标:C __________,D ____________ ;
(2)把这些点按A-B-C-D-A顺次连接起来,这个图形的面积是__________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示. 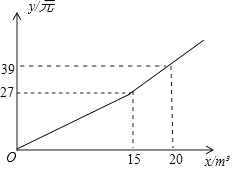
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
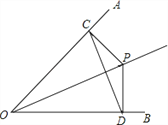
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表: 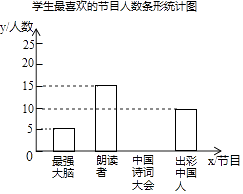
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题:
(1)x= , a= , b=;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com