
科目: 来源: 题型:
【题目】如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2 , 则S与t之间的函数关系图象大致为( )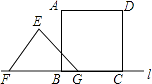
A.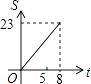
B.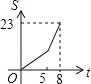
C.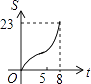
D.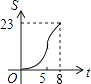
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.![]()
B.![]()
C.π
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道:同弧或等弧所对的圆周角相等.也就是,如图(1),⊙O中, ![]() 所对的圆周角∠ACB=∠ADB=∠AEB.
所对的圆周角∠ACB=∠ADB=∠AEB. 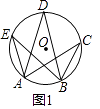
(1)已知:如图(2),矩形ABCD. 
①若AB< ![]() BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
BC,在边AD上求作点P,使∠BPC=90°.(保留作图痕迹,写出作法.)
②小明经研究发现,当AB、BC的大小关系发生变化时,①中点P的个数也会发生变化,请你就点P的个数,探讨AB与BC之间的数量关系.(直接写出结论)
创新
(2)小明经进一步研究发现:命题“若四边形的一组对边相等和一组对角相等,则这个四边形是平行四边形.”是一个假命题,并在平行四边形的基础上利用“同弧或等弧所对的圆周角相等.”作出了一个反例图形.请你利用下面如图(3)所给的□ABCD作出该反例图形.(不写作法,保留作图痕迹) 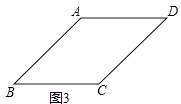
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在边BC、AC上,AE=BD,连接DE,过点E作EF⊥DE,交线段BC的延长线于点F.
(1)求证:CE=CF;
(2)若BD=![]() CE,AB=9,求线段DF的长.
CE,AB=9,求线段DF的长.
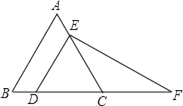
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:二次函数y=ax2+bx的图象经过点M(1,n)、N(3,n).
(1)求b与a之间的关系式;
(2)若二次函数y=ax2+bx的图象与x轴交于点A、B,顶点为C,△ABC为直角三角形,求该二次函数的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区有一块长方形水稻试验田,试验田的长、宽(如图所示,长度单位:米),试验田分两部分,一部分为水渠,另一部分为新型水稻种植田(阴影部分).
(1)用含a,b的式子表示新型水稻种植田的面积是多少平方米(结果化成最简形式);
(2)若a=30,b=40,在“农民丰收节”到来之时水稻成熟,计划先由甲型收割机收割一部分,再由乙型收割机收割剩余部分,甲型收割机收割水稻每平方米的费用为0.3元,乙型收割机收割水稻每平方米的费用为0.5元,若要收割全部水稻的费用不超过5000元,问甲型收割机最少收割多少平方米的水稻?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com