
科目: 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察图形:
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形_________________;
②线段AF与线段CE的数量关系是_________________;
(2)问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
求证:DF=2CE.

查看答案和解析>>
科目: 来源: 题型:
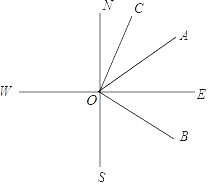
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为![]() ,第二个三角形数记为
,第二个三角形数记为![]() ,…第n个三角形数记为
,…第n个三角形数记为![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() =___________.
=___________.
查看答案和解析>>
科目: 来源: 题型:
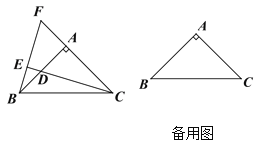
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
查看答案和解析>>
科目: 来源: 题型:
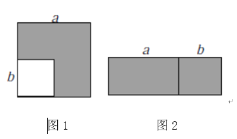
【题目】(知识情境)通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
(1)如图1,在边长为![]() 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为![]() 的小正方形
的小正方形![]() .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
.把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
(拓展探究)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
如图3是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.
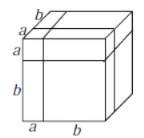
图3
(2)用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
_________________________________________________________________;
(3)已知![]() ,
,![]() ,利用上面的恒等式求
,利用上面的恒等式求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数据).
如图,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 吗?说明理由.
吗?说明理由.
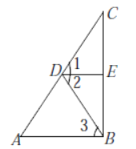
解:![]() ,理由如下:
,理由如下:
因为![]() ,
,![]() (已知)
(已知)
所以![]()
所以![]() (__________________
(__________________![]() ).
).
所以![]() (_________________________________).
(_________________________________).
所以![]() (__________________________________).
(__________________________________).
![]() (______________________________________).
(______________________________________).
因为![]() ,
,
所以![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com