（1）求证：△BDA≌△CEA；

（2）请判断△ADE是什么三角形，并说明理由．

【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1）、B（﹣3，2）、C（﹣1，4）．

①以原点O为位似中心，在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 ．
②画出△ABC绕C点顺时针旋转90°后得到的△A2B2C．

A. 120° B. 125° C. 135° D. 145°

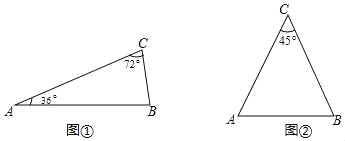
（理解）如图①，在△ABC中，∠A＝36°，∠C＝72°，请你在这个三角形中画出它的“好线”，并标出等腰三角形顶角的度数．

如图②，已知△ABC是一个顶角为45°的等腰三角形，请你在这个三角形中画出它的“好好线”，并标出所分得的等腰三角形底角的度数．

（应用）

(1)在△ABC中，已知一个内角为42°，若它只有“好线”，请你写出这个三角形最大内角的所有可能值______；

(2)在△ABC中，∠C＝27°，AD和DE分别是△ABC的“好好线”，点D在BC边上，点E在AB边上，且AD＝DC，BE＝DE，请你根据题意画出示意图，并求∠B的度数．

（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．

（2）当点P在C、D两点的外侧运动时（P点与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．

小淇同学作法如下：

（1）在直线l上任意取一点C，连接AC；

（2）作AC的中点O；

（3）以O为圆心，OA长为半径画弧交直线l于点B，如图所示；

（4）作直线AB．

则直线AB就是所要作图形．

你认为小淇的作法正确吗？如果不正确，请画出一个反例；如果正确，请给出证明．

【题目】已知关于x的方程x2﹣2（k﹣1）x+k2=0有两个实数根x1 ， x2 ．
（1）求k的取值范围；
（2）若|x1+x2|=x1x2﹣1，求k的值．

A. 120° B. 125° C. 135° D. 145°

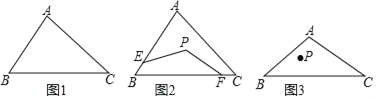
(1)已知△ABC，请用尺规在图1中△ABC内确定一个点P，使得点P到AB和BC的距离相等，且满足P到点B和点C的距离相等(不写作法，保留作图痕迹)．

(2)如图2，如果点P是(1)中求作的点，点E、F分别在边AB、BC上，且PE＝PF．

①若∠ABC＝60°，求∠EPF的度数；

②若BE＝2，BF＝8，EP＝5，求BP的长．

(3)如图3，如果点P是△ABC内一点，且点P到点B的距离是7，若∠ABC＝45°，请分别在AB、BC上求作两个点M、N，使得△PMN的周长最小(不写作法，保留作图痕迹)，则△PMN的最小值为______.