
科目: 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,若∠DCE=35°,则∠ACB=_____;若∠ACB=140°,则∠DCE=_______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A![]() 点B
点B![]() 已知
已知![]() 满足
满足![]() .
.
(1)点A的坐标为_________,点B的坐标为__________;
(2)如图1,点E为线段OB上一点,连接AE,过A作AF⊥AE,且AF=AE,连接BF交![]() 轴于点D,若点D(-1,0),求点E的坐标;
轴于点D,若点D(-1,0),求点E的坐标;
(3)在(2)的条件下,如图2,过E作EH⊥OB交AB于H,点M是射线EH上一点(点M不在线段EH上),连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,探究线段MN与OM的关系,并说明理由。
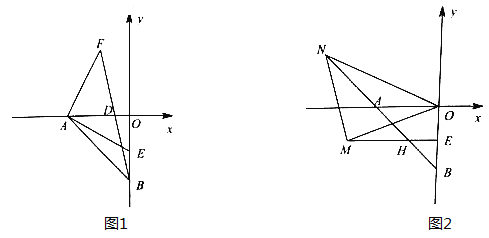
查看答案和解析>>
科目: 来源: 题型:
【题目】数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)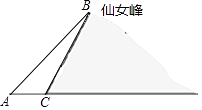
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题: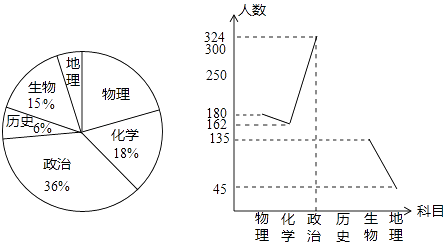
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com