
科目: 来源: 题型:
【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图一,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上,
①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)若∠BAC![]() 60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】先填写表,通过观察后再回答问题:
a | 0 | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| 0 | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ,y= ;
(2)从表格中探究a与![]() 数位变化可以发现:当被开方数a每扩大100倍时,
数位变化可以发现:当被开方数a每扩大100倍时,![]() 扩大_________倍,请你利用这个规律解决下面两个问题:
扩大_________倍,请你利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ;
;
②已![]() ,若
,若![]() ,用含m的代数式表示n,则n= ;
,用含m的代数式表示n,则n= ;
(3)请根据表格提示,试比较![]() 与a的大小.
与a的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
组别 | 分组 | 频数 | 频率 |
1 | 15~25 | 7 | 0.14 |
2 | 25~35 | a | 0.24 |
3 | 35~45 | 20 | 0.40 |
4 | 45~55 | 6 | b |
5 | 55~65 | 5 | 0.10 |
注:这里的15~25表示大于等于15同时小于25.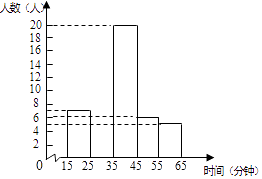
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.

(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.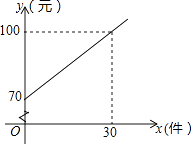
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3( )
得∠2=∠3( )
所以AE//_______( )
得∠4=∠F( )
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com