
科目: 来源: 题型:
【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.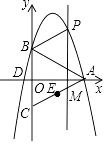
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
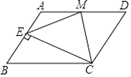
【题目】如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.
(1)求平行四边形ABCD的面积S;
(2)求证:∠EMC=2∠AEM.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年12月29日至31日,黔南州第十届旅游产业发展大会在“中国长寿之乡”﹣﹣罗甸县举行,从中寻找到商机的人不断涌现,促成了罗甸农民工返乡创业热潮.某“火龙果”经营户有A、B两种“火龙果”促销,若买2件A种“火龙果”和1件B种“火龙果”,共需120元;若买3件A种“火龙果”和2件B种“火龙果”,共需205元.
(1)设A,B两种“火龙果”每件售价分别为a元、b元,求a、b的值;
(2)B种“火龙果”每件的成本是40元,根据市场调查:若按(1)中求出的单价销售,该“火龙果”经营户每天销售B种“火龙果”100件;若销售单价每上涨1元,B种“火龙果”每天的销售量就减少5件.
①求每天B种“火龙果”的销售利润y(元)与销售单价x(元)之间的函数关系?
②求销售单价为多少元时,B种“火龙果”每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题原型)
如图①,AB∥CD,点M在直线AB、CD之间,则∠M=∠B+∠D,小明解决上述问题的过程如下:
如图②,过点M作MN∥AB
则∠B=_______(_______)
∵AB∥CD,(已知)
MN∥AB(辅助线的做法)
∴MN∥CD(______)
∴∠______=∠D(______)
∴∠B+∠D=∠BMD
请完成小明上面的过程.

(问题迁移)
如图③,AB∥CD,点M与直线CD分别在AB的两侧,猜想∠M、∠B、∠D之间有怎样的数量关系,并加以说明.
(推广应用)
(1)如图④,AB∥CD,点M在直线AB、CD之间,∠ABM的平分线与∠CDM的平分线交于点N,∠M=96°,则∠N=_____°;
(2)如图⑤,AB∥CD,点M与直线CD分别在AB的两侧,∠ABM的平分线与∠CDM的平分线交于点N,∠N=25°,则∠M=______°;
(3)如图⑥,AB∥CD,∠ABG的平分线与∠CDE的平分线交于点M,∠G=78°,∠F=64°,∠E=64°,则∠M=_______°.

查看答案和解析>>
科目: 来源: 题型:
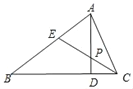
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)= ![]() .
.
例如:tan15°=tan(45°﹣30°)= ![]() =
= 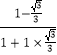 =
= ![]()
= ![]() =
= ![]() =2﹣
=2﹣ ![]() .
.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据 ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)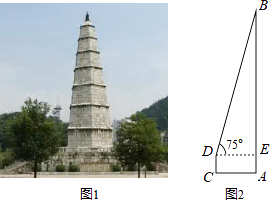
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从数轴上的原点开始,先向左移动2cm到达A点,再向左移动4cm到达B点,然后向右移动10cm到达C点.
![]()
(1)用1个单位长度表示1cm,请你在题中所给的数轴上表示出A、B、C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm;
(3)若点B以每秒3cm的速度向左移动,同时A、C点以每秒lcm、5cm的速度向右移动,设移动时间为t(t>0)秒,试探究CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com