【题目】点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：ab＞0，其中正确的是（ ）

A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁

（1）画出△A′B′C′；

（2）画出△ABC的高，即线段BD；

（3）连接AA′、 CC′，那么AA′与CC′的关系是________；线段AC扫过图形的面积为____．

进价与售价折线图(单位：元/斤)

实际销售量表(单位：斤)

则下列推断不合理的是( )

A. 该商品周一的利润最小

B. 该商品周日的利润最大

C. 由一周中的该商品每天售价组成的这组数据的众数是4(元/斤)

D. 由一周中的该商品每天进价组成的这组数据的中位数是3(元/斤)

(1)求每台A型电脑和B型电脑的销售利润；

(2)该商店计划一次购进两种型号的电脑共50台，其中A型电脑的进货量不少于14台，B型电的进货量不少于A型电脑的2倍，那么该商店有几种进货方案?该商场购进A型、B型电脑各多少台，才能使销售总利润最大?

(3)实际进货时，厂家对A型电脑出厂价下调m (0<m<100)元，若商店保持两种电脑的售价不变，请你根据以上信息及(2)中条件，设计出使这50台电脑销售总利润最大的进货方案．

【题目】如图1，已知抛物线y=﹣ x2﹣ x+c与x轴相交于A、B两点（B点在A点的左侧），与y轴相交于C点，且AB=10．

（1）求这条抛物线的解析式；
（2）如图2，D点在x轴上，且在A点的右侧，E点为抛物线上第二象限内的点，连接ED交抛物线于第二象限内的另外一点F，点E到y轴的距离与点F到y轴的距离之比为3：1，已知tan∠BDE= ，求点E的坐标；
（3）如图3，在（2）的条件下，点G由B出发，沿x轴负方向运动，连接EG，点H在线段EG上，连接DH，∠EDH=∠EGB，过点E作EK⊥DH，与抛物线相应点E，若EK=EG，求点K的坐标．

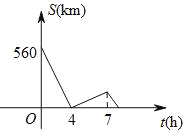
A. ①② B. ①③ C. ①④ D. ①③④

(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?

(2)如果工厂招聘n(0<n<10)名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案？

(3)在(2)的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W(元)尽可能的少?

【题目】现计划把一批货物用一列火车运往某地已知这列火车可挂A，B两种不同规格的货车厢共40节，使用A型车厢每节费用6000元，使用B型车厢每节费用为8000元．

设运送这批货物的总费用为y元，这列火车挂A型车厢x节，写出y关于x的函数表达式，并求出自变量x的取值范围；

已知A型车厢数不少于B型车厢数，运输总费用不低于276000元，问有哪些不同运送方案？

【题目】已知：O是坐标原点，P（m，n）（m＞0）是函数y= （k＞0）上的点，过点P作直线PA⊥OP于P，直线PA与x轴的正半轴交于点A（a，0）（a＞m）．设△OPA的面积为s，且s=1+ ．

（1）当n=1时，求点A的坐标；
（2）若OP=AP，求k的值；
（3）设n是小于20的整数，且k≠ ，求OP2的最小值．