【题目】综合题，如图，正方形ABCD。
（1）请在图①中作两条直线，使它们将正方形ABCD的面积三等分；

（2）如图②，在矩形ABCD中，AB=6，BC=9，在图②中过顶点A作两条直线，使它们将矩形ABCD的面积三等分，井说明理由；

（3）如图③，农博园有一块不规则的五边形ABCDE空地，其中AB∥CD、AE∥BC，AB=AC=100米，AE=160米，BC=120米，CD=62.5米，根据视觉效果和花期特点，农博园设计部门想在这片空地种上等面积的三种不同的花，要求从入口A点处修两条笔直的小路（小路的面积忽略不计）方便游客赏花，两条小路将这块地面积三等分．请通过计算画图说明其设计部们能否实现，若能实现请确定小路尽头的位置．

【题目】填空：如图，于点D，于点E，，，求的度数．

解：∵，（已知）

∴ （ ）

∴（ ）

∴（ ）//（ ）（ ）

∴（ ）（ ）

∵（ ）

∴（ ）

∴（ ）//（ ）（ ）

∴（ ）

∵（ ）

∴（ ）=（ ）（等式性质）

【题目】如图，抛物线y= x2+bx+c经过A（﹣1，0），C（2，﹣3）两点，与y轴交于点D，与x轴交于另一点B．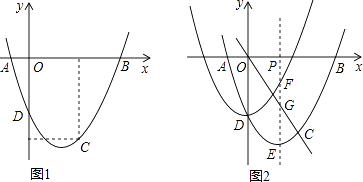

（1）求此抛物线的解析式及顶点坐标；
（2）若将此抛物线平移，使其顶点为点D，需如何平移？写出平移后抛物线的解析式；
（3）过点P（m，0）作x轴的垂线（1≤m≤2），分别交平移前后的抛物线于点E，F，交直线OC于点G，求证：PF=EG．

根据表中，父亲还给小明出了下面几个问题，你和小明一起回答．

（1）表中自变量是________；因变量是_________；在地面上（即时）时，温度是_________℃；

（2）如果用表示距离地面的高度，用表示温度，则满足与关系的式子为_____________；

（3）计算出距离地面6千米的高空温度是多少？

【题目】如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．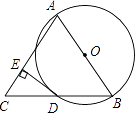

（1）求证：DE为⊙O的切线；
（2）若⊙O的半径为5，∠BAC=60°，求DE的长．

【题目】小晗家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，在正常情况下，小晗按下任意一个开关均可打开对应的一盏电灯，既可三盏、两盏齐开，也可分别单盏开．因刚搬进新房不久，不熟悉情况．

（1）若小晗任意按下一个开关，正好楼梯灯亮的概率是多少？
（2）若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．

【题目】某学校期末考试要给学生印制复习资料若干份，印刷厂有甲、乙两种收费方式，除按印刷份数收取印刷费用外，甲种方式还收取制版费，而乙种不需要，两种印刷方式的费用y（元）与印刷份数x（份）之间的函数关系如图所示：

（1）填空：甲种收费方式的函数关系式是 ， 乙种收费方式的函数关系式是 ．
（2）若需印刷100﹣400份（含100和400）份复习资料，选择哪种印刷方式比较合算．

（1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE=AF；

（2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE=AF吗？请利用图②说明理由．

【题目】小明想用镜子测量一棵松树的高度，但因树旁有一条河，不能测量镜子与树之间的距离，于是他两次利用镜子，如图所示，第一次他把镜子放在C点，人在F点时正好在镜子中看到树尖A；第二次把镜子放在D点，人在G点正好看到树尖A．已知小明的眼睛距离地面1.70m，量得CD=12m，CF=1.8m，DH=3.8m．请你求出松树的高．

一般地，n个相同的因数a相乘记为an，记为an．如2×2×2=23=8，此时，3叫做以2为底8的对数，记为log28（即log28=3）．一般地，若an=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为logab（即logab=n）．如34=81，则4叫做以3为底81的对数，记为log381（即log381=4）．

（1）计算以下各对数的值：

log24= ，log216= ，log264= ．

（2）观察（1）中三数4、16、64之间满足怎样的关系式，log24、log216、log264之间又满足怎样的关系式 ．

（3）由（2）的结果，你能归纳出一个一般性的结论吗？

logaM+logaN= ；（a＞0且a≠1，M＞0，N＞0）

（4）根据幂的运算法则：anam=an+m以及对数的含义证明上述结论．