
科目: 来源: 题型:
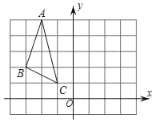
【题目】如图,△ABC在平面直角坐标系中,A(﹣2,5),B(﹣3,2),C(﹣1,1).
(1)请画出△ABC关于y轴的对称图形△A′B′C′,其中A点的对应点是A′,B点的对应点是B′,C点的对应点是C′,并写出A′,B′,C′三点的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下面是一周中每天的生产情况记录表(超过200辆记为正、不足200辆记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(1)根据记录可知前两天共生产 辆自行车;
(2)产量最多的一天比产量最少的一天多生产 辆自行车;
(3)该厂实行计件工资制,每生产一辆自行车可得80元.若超额完成任务,则超额部分每辆再奖20元;若没有完成计划工作量,则每少生产一辆扣20元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目: 来源: 题型:
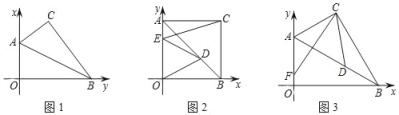
【题目】在平面直角坐标系中,点A(0,4),B(m,0)在坐标轴上,点C,O关于直线AB对称,点D在线段AB上.
(1)如图1,若m=8,求AB的长;
(2)如图2,若m=4,连接OD,在y轴上取一点E,使OD=DE,求证:CE=![]() DE;
DE;
(3)如图3,若m=4![]() ,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
,在射线AO上裁取AF,使AF=BD,当CD+CF的值最小时,请在图中画出点D的位置,并直接写出这个最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A.∠B=50° ,∠C=40°
B.∠B=∠C=45°
C.∠A,∠B,∠C的度数比为5:3:2
D.∠A-∠B=90°
查看答案和解析>>
科目: 来源: 题型:
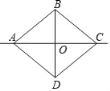
【题目】如图,四边形ABCD沿直线AC对折后重合,如果AC,BD交于O,AB∥CD,则结论①AB=CD,②AD∥BC,③AC⊥BD,④AO=CO,⑤AB⊥BC,其中正确的结论是___(填序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.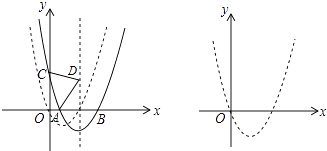
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .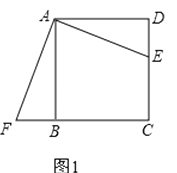
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.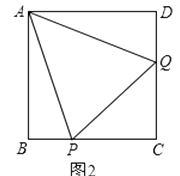
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 . 
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com