
【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
【答案】(1)P点坐标为(![]() ,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
【解析】
(1)根据题意画坐标系描点,根据两点之间线段最短,求直线AB解析式,与x轴交点即为所求点P.
(2)①作点A关于x轴的对称点A',根据轴对称性质有∠APO=∠A'PO,所以此时P、A'、B在同一直线上.求直线A'B解析式,与x轴交点即为所求点P.
②法一,根据坐标系里三角形面积等于水平长(右左两顶点的横坐标差)与铅垂高(上下两顶点的纵坐标差)乘积的一半,求得△PAB的面积为12,进而求得△QAP的铅垂高等于6,再得出直线BQ上的点E坐标为(2,8)或(2,﹣4),求出直线BQ,即能求出点Q坐标.法二,根据△QAB与△PAB同以AB为底时,高应相等,所以点Q在平行于直线AB、且与直线AB距离等于P到直线AB距离的直线上.这样的直线有两条,一条即过点P且与AB平行的直线,另一条在AB上方,根据平移距离相等即可求出.所求直线与y轴交点即点Q.
(1)∵两点之间线段最短,∴当A、P、B在同一直线时,PA+PB=AB最短(如图1).
设直线AB的解析式为:y=kx+b.
∵A(2,2),B(4,﹣3),∴![]() ,解得:
,解得: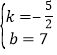 ,∴直线AB:y
,∴直线AB:y![]() x+7.
x+7.
当![]() x+7=0时,得:x
x+7=0时,得:x![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).
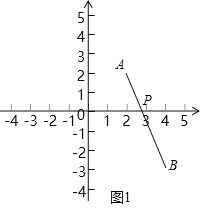
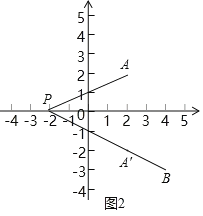
(2)①作点A(2,2)关于x轴的对称点A'(2,﹣2).
根据轴对称性质有∠APO=∠A'PO.
∵∠APO=∠BPO,∴∠A'PO=∠BPO,∴P、A'、B在同一直线上(如图2).
设直线A'B的解析式为:y=k'x+b'.
![]() ,解得:
,解得: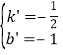 ,∴直线A'B:y
,∴直线A'B:y![]() x﹣1.
x﹣1.
当![]() x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
②存在满足条件的点Q.
法一:设直线AA'交x轴于点C,过B作BD⊥直线AA'于点D(如图3),∴PC=4,BD=2,∴S△PAB=S△PAA'+S△BAA'![]() .
.
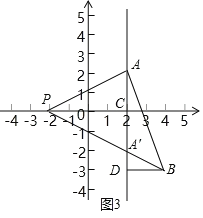
设BQ与直线AA'(即直线x=2)的交点为E(如图4).
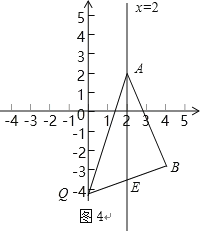
∵S△QAB=S△PAB,则S△QAB![]() 2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
设直线BQ解析式为:y=ax+q.则:
![]() 或
或![]()
解得: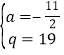 或
或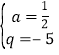 ,∴直线BQ:y
,∴直线BQ:y![]() 或y
或y![]() ,∴Q点坐标为(0,19)或(0,﹣5).
,∴Q点坐标为(0,19)或(0,﹣5).
法二:∵S△QAB=S△PAB,∴△QAB与△PAB以AB为底时,高相等,即点Q到直线AB的距离=点P到直线AB的距离.
i)若点Q在直线AB下方,则PQ∥AB.
设直线PQ:y![]() x+c,把点P(﹣2,0)代入,解得:c=﹣5,y
x+c,把点P(﹣2,0)代入,解得:c=﹣5,y![]() x﹣5,即Q(0,﹣5);
x﹣5,即Q(0,﹣5);
ii)若点Q在直线AB上方.
∵直线y![]() x﹣5向上平移12个单位得直线AB:y
x﹣5向上平移12个单位得直线AB:y![]() x+7,∴把直线AB:y
x+7,∴把直线AB:y![]() x+7再向上平移12个单位得直线AB:y
x+7再向上平移12个单位得直线AB:y![]() x+19,∴Q(0,19).
x+19,∴Q(0,19).
综上所述:y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2(________)
∵AC∥DE(已知)
∴∠1=∠3(________)
故∠2=∠3(________)
∵DF∥AE(已知)
∴∠2=∠5(________)
∴∠3=∠4(________)
∴DE平分∠BDE(________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)在图中画出△ABC与关于y轴对称的图形△A1B1C1,并写出顶点A1、B1、C1的坐标;
(2)若将线段A1C1平移后得到线段A2C2,且A2(a,2),C2(-2,b),求a+b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是 .
(2)根据你添加的条件,再写出图中的一对全等三角形 .(只要求写出一对全等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
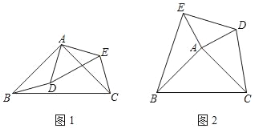
【题目】已知,等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°.
(1)如图1,求证:DB=CE;
(2)如图2.求证:S△ACD=S△ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com