【题目】如图，菱形ABCD的对角线AC与BD交于点O，AC=6，BD=8．动点E从点B出发，沿着B﹣A﹣D在菱形ABCD的边上运动，运动到点D停止．点F是点E关于BD的对称点，EF交BD于点P，若BP=x，△OEF的面积为y，则y与x之间的函数图象大致为（ ）

A.
B.
C.
D.

（1） （2）

（3） （4）

【题目】如图，平行四边形ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于 的一元二次方程 的两个根，且OA＞OB

（1）求cos∠ABC的值。
（2）若E为x轴上的点，且 ，求出点E的坐标，并判断△AOE与△DAO是否相似？请说明理由

（1）如图1，求证：A、G、E、F四点围成的四边形是菱形；

（2）如图2，点N是线段BC的中点，且ON＝OD，求折痕FG的长．

【题目】某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为 ，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求y与x的关系式.
（2）当x取何值时，y的值最大？
（3）如果公司想要在这段时间内获得 元的销售利润，销售单价应定为多少元？

通常情况下、用两种不同的方法计算同一图形的面积，可以得到一个恒等式.

（1）如图 1，请你写出之间的等量关系是

（知识应用）

（2）根据（1）中的结论，若，则

（知识迁移）

类似地，用两种不同的方法计算同一几何体的情况，也可以得到一个恒等式.如图 是边长为的正方体，被如图所示的分割成 块．

（3）用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式可以是

（4）已知，，利用上面的规律求的值．

【题目】某口罩加工厂有两组工人共人，组工人每人每小时可加工口罩只，组工人每小时可加工口罩只,两组工人每小时一共可加工口罩只.

（1）求两组工人各有多少人？

（2）由于疫情加重，两组工人均提高了工作效率，一名组工人和一名组工人每小时共可生产口罩只，若两组工人每小时至少加工只口罩，那么组工人每人每小时至少加工多少只口罩？

【题目】仔细阅读下面解方程组的方法,然后解决有关问题:解方程组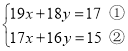时，如果直接消元，那将会很繁琐，若采用下面的解法,则会简单很多.

解：①-②，得：2x+2y=2，即x+y=1③

③×16，得：16x+16y=16④

②-④，得：x=-1

将x=-1

代入③得：y=2

∴原方程组的解为：

（1）请你采用上述方法解方程组：

（2）请你采用上述方法解关于x，y的方程组，其中．

【题目】小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B,F,D在同一条直线上）。一直小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据： ≈1.732， ≈1.414，结果保留整数）

3+2＝2+2+1＝()2+2+1＝(+1)2；

5+2＝2+2+3＝()2+2××+()2＝(+)2

(1)请仿照上面式子的变化过程，把下列各式化成另一个式子的平方的形式：

①4+2；②6+4

(2)若a+4＝(m+n)2，且a，m，n都是正整数，试求a的值．