
科目: 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )

A. 3对 B. 2对 C. 1对 D. 0对
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.
(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】填空,完成下列说理过程
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
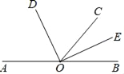
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校计划购买20张书柜和一批书架(书架不少于20只),现从A、B两家超市了解到:同型号的产品价格相同,书柜每张210元,书架每只70元,A超市的优惠政策为每买一张书柜赠送一只书架,B超市的优惠政策为所有商品八折.
(1)若规定只能到其中一个超市购买所有物品,什么情况下到A超市购买合算?
(2)若学校想购买20张书柜和100个书架,且可到两家超市自由选购.你认为至少要准备多少货款,请用计算的结果来验证你的说法.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面的证明:
已知:如图,点D,E,F分别在线段AB,BC,AC上,连接DE、EF,DM平分∠ADE交EF于点M,∠1+∠2=180°.
求证: ∠B =∠BED.

证明:∵∠1+∠2=180°(已知),
又∵∠1+∠BEM=180°( ),
∴∠2=∠BEM( ),
∴DM∥______(_________________________________________).
∴∠ADM =∠B(_________________________________________),
∠MDE =∠BED(_______________________________________).
又∵DM平分∠ADE (已知),
∴∠ADM =∠MDE ( ).
∴∠B =∠BED(等量代换).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com