【题目】如图所示，在△ABC中，AB=AC，M、N分别是AB、AC的中点，D、E为BC上的点，连接DN、EM，若AB=5cm，BC=8cm，DE=4cm，则图中阴影部分的面积为( )

A.1cm2
B.1.5cm2
C.2cm2
D.3cm2

【题目】已知，如图，、是直线，，，.与平行吗？为什么？

解：，理由如下：

∵（已知）

∴（ ）

∵（已知）

∴_________（ ）

∵（已知）

∴（ ）

即

∴_________（等量代换）

∴（ ）

(1)服药后几时血液中含药量最高？每毫升血液中含多少微克？

(2)在服药几时内，每毫升血液中含药量逐渐升高？在服药几时后，每毫升血液中含药量逐渐下降？

(3)服药后14 h时，每毫升血液中含药量是多少微克？

(4)如果每毫升血液中含药量为4微克及以上时，治疗疾病有效，那么有效时间为几时？

（1）如图1，求∠EFB的度数；

（2）若三角板ACB的位置保持不动，将三角板CDE绕其直角顶点C顺时针方向旋转．

①当旋转至如图2所示位置时，恰好CD∥AB，则∠ECB的度数为　 　；

②若将三角板CDE继续绕点C旋转，直至回到图1位置．在这一过程中，是否还会存在△CDE其中一边与AB平行？如果存在，请你画出示意图，并直接写出相应的∠ECB的大小；如果不存在，请说明理由．

【题目】“差之毫厘，失之千里”是一句描述开始时虽然相差很微小，结果会造成很大的误差或错误的成语.现实中就有这样的实例，如步枪在瞄准时的示意图如图，从眼睛到准星的距离OE为80cm，眼睛距离目标为200m，步枪上准星宽度AB为2mm，若射击时，由于抖动导致视线偏离了准星1mm，则目标偏离的距离为（ ）cm．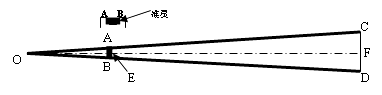

A.25
B.50
C.75
D.100

对于任意一个三位数正整数n，如果n的各个数位上的数字互不相同，且都不为零，那么称这个数为“陌生数”，将一个“陌生数”的三个数位上的数字交换顺序，可以得到5个不同的新“陌生数”，把这6个陌生数的和与111的商记为M(n).例如n=123，可以得到132.213.231.312.321这5个新的“陌生数”，这6个“陌生数”的和为123＋132＋213＋231＋312＋321=1332，因为，所以M(123)=12.

(1)计算：M(125)和M(361)的值；

(2)设s和t都是“陌生数”，其中4和2分别是s的十位和个位上的数字，2和5分别是t的百位和个位上的数字，且t的十位上的数字比s的百位上的数字小2；规定：.若，则k的值是多少？

【题目】如图，在平面直角坐标系中，顶点为（2，﹣1）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，3），连接AB．

（1）求此抛物线的解析式；
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明；
（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

【题目】某数学兴趣小组开展了一次活动，过程如下：如图1，等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将三角板中含45°角的顶点放在A上，斜边从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．

（1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；
（2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2 ． 同组的小颖和小亮随后想出了两种不同的方法进行解决：
小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）；
小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；
请你从中任选一种方法进行证明．
（3）小敏继续旋转三角板，请你继续研究：当135°＜α＜180°时（如图4），等量BD2+CE2=DE2是否仍然成立？请作出判断，不需要证明．

（1）整理、描述数据：按如分数段整理、描述这两组样本数据（请补全表格）：

（说明：成绩80分及以上为生产技能优秀，70-79分为生产技能良好，60-69分为生产技能合格，60分以下为生产技能不合格）

分析数据：两组样本数据的平均数、中位数、众数如表所示（请补全表格）：

得出结论：

（2）估计乙部门生产技能优秀的员工人数为__________；

（3）你认为__________部门员工的生产技能水平较高，说明理由（至少从两个不同的角度说明推断的合理性）．

【题目】如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元．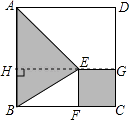

（1）探究1：如果木板边长为1米，FC= 米，则一块木板用墙纸的费用需元；
（2）探究2：如果木板边长为2米，正方形EFCG的边长为x米，一块木板需用墙纸的费用为y元，
①用含x的代数式表示y（写过程）．
②如果一块木板需用墙纸的费用为225元，求正方形EFCG的边长为多少米？