
科目: 来源: 题型:
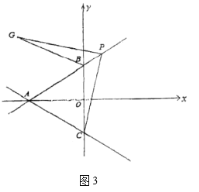
【题目】如图,在直角坐标系内,正方形如图摆放,已知顶点 A(a,0),B(0,b) ,则顶点C的坐标为( )
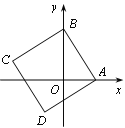
A.(-b,a b)B.(-b,b - a)C.(-a,b - a)D.(b,b -a)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根.
(2)是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2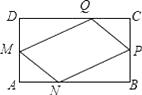
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围.
(2)若a=400,求S的最大值,并求出此时x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】体考在即,初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查,制作出如图所示的统计图,其中1班有50人.(注:30分以上为达标,满分50分)根据统计图,解答下面问题:
(1)初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少?
(2)若除初三(1)班外其余班级学生体育考试成绩在30﹣﹣40分的有120人,请补全扇形统计图;(注:请在图中分数段所对应的圆心角的度数)
(3)如果要求全年级学生的体育达标率不低于90%,试问在本次调查中,该年级全体学生的体育达标率是否符合要求?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 和点
和点![]() 关于原点对称,点
关于原点对称,点![]() 是直线
是直线![]() 位于
位于![]() 轴右侧部分图象上一点,连接
轴右侧部分图象上一点,连接![]() ,已知
,已知![]() .
.
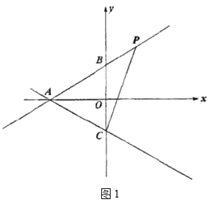
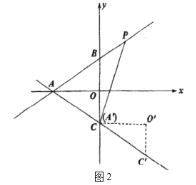
(1)求直线![]() 的解析式;
的解析式;
(2)如图2,![]() 沿着直线
沿着直线![]() 平移得
平移得![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合.点
重合.点![]() 为直线
为直线![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出
的值最小时,请求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图3,将![]() 沿直线
沿直线![]() 是翻折得
是翻折得![]() 点
点![]() 为平面内任意一动点,在直线
为平面内任意一动点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形是矩形;若存在,请直接写出点
为顶点的四边形是矩形;若存在,请直接写出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)(阅读理解)
如图(1),AD是△ABC的中线,作△ABC的高AH.
∵AD是△ABC的中线
∴BD=CD
∵S△ABD=![]() BDAH,S△ACD=
BDAH,S△ACD=![]() CDAH
CDAH
∴S△ABD S△ACD(填:<或>或=)
(2)(结论拓展)
△ABC中,D是BC边上一点,若![]() ,则
,则![]() =
=
(3)(结论应用)
如图(3),请你将△ABC分成4个面积相等的三角形(画出分割线即可)
如图(4),BE是△ABC的中线,F是AB边上一点,连接CF交BE于点O,若![]() ,则
,则![]() = .说明你的理由
= .说明你的理由
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年1月重庆湖童时装周在重庆渝北举行了八场走秀,云集了八大国内外潮童品牌,不仅为大家带来了一场品牌走秀盛会,更让人们将目光转移到了![]() 后、
后、![]() 后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进
后童模群体身上,开启服装新秀湖流.某大型商场抓住这次商机购进![]() 两款新童装进行试销售,该商场用
两款新童装进行试销售,该商场用![]() 元购买
元购买![]() 款童装,用
款童装,用![]() 元购买
元购买![]() 款童装,且每件
款童装,且每件![]() 款童装进价与每件
款童装进价与每件![]() 款童装进价相同,购买
款童装进价相同,购买![]() 款童装的数量比
款童装的数量比![]() 款童装的数量少
款童装的数量少![]() 件,若该商场本次以每件
件,若该商场本次以每件![]() 款童装按进价加价
款童装按进价加价![]() 元进行销售,每件
元进行销售,每件![]() 款童装按进价加价
款童装按进价加价![]() 进行销售,全部销售完.
进行销售,全部销售完.
(1)求购进![]() 两款童装各多少件?
两款童装各多少件?
(2)春节期间该商场按上次进价又购进与上一次一样数量的![]() 两款童装,并展开了降价促销活动,在促销期间,该商场将每件
两款童装,并展开了降价促销活动,在促销期间,该商场将每件![]() 款童装按进价提高
款童装按进价提高![]() 进行销售,每件
进行销售,每件![]() 款童装按上次售价降低
款童装按上次售价降低![]() 销售.结果全部销售完后销售利润比上次利润少了
销售.结果全部销售完后销售利润比上次利润少了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() 将直线
将直线![]() 向上平移
向上平移![]() 个单位得直线
个单位得直线![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() 且点
且点![]() 的横坐标为
的横坐标为![]()

(1)求直线![]() 的解析式;
的解析式;
(2)连接![]() 求
求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】小数在数学外小组活动中遇到这样一个问题:如果α、β都为锐角,且tanα= ![]() ,tanβ=
,tanβ= ![]() .求α+β的度数.
.求α+β的度数.
(1)小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=°.
(2)请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题背景)
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D
![]()


(简单应用)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,试求∠P的度数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com