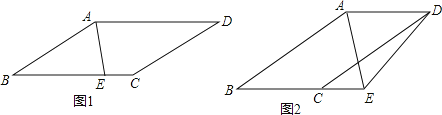
（1）如图1，当点E在线段BC上时，求证：∠BAE=∠BEA．

（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE=3∠CDE，∠AED=60°．

①求证∠ABC=∠ADC；

②求∠CED的度数．

（1）求该网店购进甲、乙两种型号口罩各多少袋？

（2）该网店第二次以原价购进甲、乙两种型号口罩，购进乙种型号口罩袋数不变，而购进甲种型号口罩袋数是第一次的2倍．甲种口罩按原售价出售，而乙种口罩让利销售．若两种型号的口罩都售完，要使第二次销售活动获利不少于3680元，乙种型号的口罩最低售价为每袋多少元？

【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= ． 例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= ．
（Ⅰ）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
求证：对任意一个完全平方数m，总有F（m）=1；
（Ⅱ）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；
（Ⅲ）在（2）所得“吉祥数”中，求F（t）的最大值．

（1）指出旋转中心，并求出旋转的度数；

（2）求出∠BAE的度数和AE的长．

A. 24 B. 28 C. 32 D. 36

（1）若点F在边CD上，如图1．

①证明：∠DAH=∠DCH；

②猜想：△GFC的形状并说明理由．

（2）取DF中点M，连接MG．若MG=2.5，正方形边长为4，求BE的长．

【题目】对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F（123）=6．
（1）计算：F（243），F（617）；
（2）若s，t都是“相异数”，其中s=100x+32，t=150+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k= ，当F（s）+F（t）=18时，求k的最大值．

（1）如图2，当点G和点M重合时，求证：四边形DMEN是菱形；

（2）如图1，当点G和点M、C不重合时，求证：DG＝DN．

【题目】阅读理解：用“十字相乘法”分解因式2x2﹣x﹣3的方法．
（i）二次项系数2=1×2；
（ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；

1×3+2×（﹣1）=1 1×（﹣1）+2×3=5 1×（﹣3）+2×1=﹣1 1×1+2×（﹣3）=﹣5
（iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．
即：（x+1）（2x﹣3）=2x2﹣3x+2x﹣3=2x2﹣x﹣3，则2x2﹣x﹣3=（x+1）（2x﹣3）．
像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2+5x﹣12= ．