
科目: 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.当AB与BC满足___________条件时,四边形AEOF正方形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】探索题:(x-1)((x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)=x5-1.
(1)观察以上各式并猜想:
①(x-1)(x6+x5+x4+x3+x2+x+1)=________________________;
②(x-1)(xn+xn-1+xn-2+…+x3+x2+x+1)= ________________________;
(2)请利用上面的结论计算:
①(-2)50+(-2)49+(-2)48+…+(-2)+1
②若x1007+x1006+…+x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系:

(1)在这个变化过程中自变量是_________,因变量是___________;
(2)小李_________时到达离家最远的地方,此时离家_________km;
(3)分别求出在1≤t≤2时和2≤t≤4时小李骑自行车的速度;
(4)请直接写出小李何时与家相距20km?
查看答案和解析>>
科目: 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
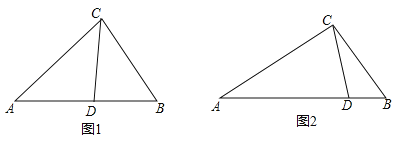
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.

(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=_____________(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com