
科目: 来源: 题型:
【题目】在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程![]() 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程” ![]() 的根的情况是______(填序号):
的根的情况是______(填序号):
①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
(2)如图,AD为⊙O的直径,BC为弦, BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程” ![]() 的解;
的解;

(3)若x=![]() 是“△ABC的☆方程”
是“△ABC的☆方程” ![]() 的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且![]() ,求方程的另一个根.
,求方程的另一个根.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数![]() (a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④
(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④![]() <a<
<a<![]() ;⑤b>c.其中正确结论个数( )
;⑤b>c.其中正确结论个数( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图, 请根据图中提供的信息,完成下列问题:
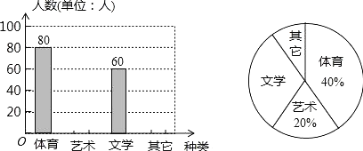
(1)此次共调查了 人;
(2)求文学社团在扇形统计图中所占圆心角为 度;
(3)请将条形统计图补充完整;
(4)若该校有 1500 名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
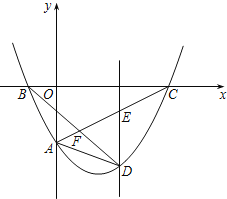
【题目】如图,经过点A(0,﹣2)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,D为第四象限内抛物线上一点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,D为第四象限内抛物线上一点.
(1)求抛物线的解析式;
(2)过点D作y轴的平行线交AC于点E,若AD=AE,求点D的坐标;
(3)连接BD交AC于点F,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
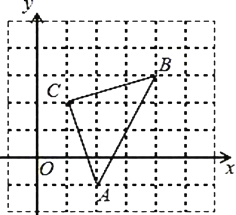
【题目】如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:A ,B ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(3)若AB边上有一点M(a,b),平移后对应的点M1的坐标为________________;
(4)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE 交 AD 于点 F.
(1)求证:△BDF 是等腰三角形;
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;
②若 AB=6,AD=8,则 FG 的长为_____.


查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有________

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某城市接到台风警报,在该市正南方向![]() 的
的![]() 处有一台风中心,沿
处有一台风中心,沿![]() 方向以
方向以![]() 的速度移动,已知城市
的速度移动,已知城市![]() 到
到![]() 的距离
的距离![]() .
.
(1)台风中心经过多长时间从![]() 移动到
移动到![]() 点?
点?
(2)已知在距台风中心![]() 的圆形区域内都会受到不同程度的影响,若在点
的圆形区域内都会受到不同程度的影响,若在点![]() 的工作人员早上6:00接到台风警报,台风开始影响到台风结束影响要做预防工作,则他们要在什么时间段内做预防工作?
的工作人员早上6:00接到台风警报,台风开始影响到台风结束影响要做预防工作,则他们要在什么时间段内做预防工作?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com