
科目: 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
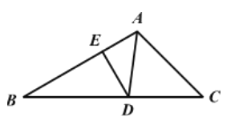
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售A,B两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.

(1)若该商场计划购进两种多媒体教学设备若干套,共需124万元,全部销售后可获毛利润36万元.则该商场计划购进A,B两种品牌的多媒体教学设备各多少套?
(2)通过市场调研,该商场决定在(1)中所购总数量不变的基础上,减少A种设备的购进数量,增加B种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过120万元,且全部销售后可获毛利润不少于33.6万元.问有几种购买方案?并写出购买方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.

(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,且在y轴的右侧。过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.
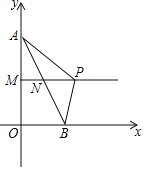
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形![]() 的面积为20,对角线
的面积为20,对角线![]() ,
,![]() 交于点
交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为( )
的面积为( )
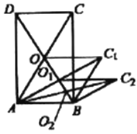
A.![]() B.
B.![]() C.
C.![]() D.45
D.45
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.

(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠AOC的度数。
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系中,A(0,4),点P从原点O开始向x轴正方向运动,设P点横坐标为m,以点P为圆心,PO为半径作⊙P交x 轴另一点为C,过点A作⊙P的切线交 x轴于点B,切点为Q.
(1)如图1,当B点坐标为(3,0)时,求m;
(2)如图2,当△PQB为等腰三角形时,求m;
(3)如图3,连接AP,作PE⊥AP交AB于点E,连接CE,求证:CE是⊙P的切线;
(4)若在x轴上存在点M(8,0),在点P整个运动过程中,求MQ的最小值.
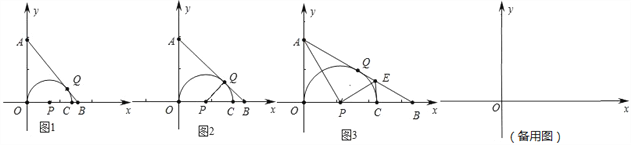
查看答案和解析>>
科目: 来源: 题型:
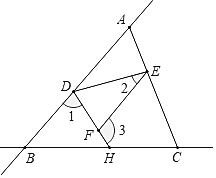
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=![]() 求∠3的度数(用含
求∠3的度数(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com