
科目: 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
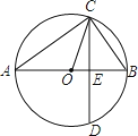
(1)求证:∠ACO=∠BCD;
(2)若BE=3,CD=8,求AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).
(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
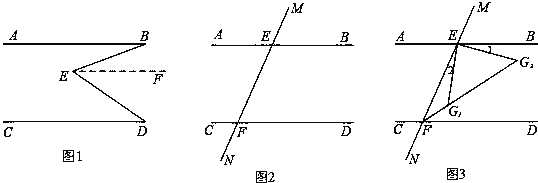
查看答案和解析>>
科目: 来源: 题型:
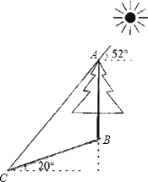
【题目】如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用)
查看答案和解析>>
科目: 来源: 题型:
【题目】“读书破万卷,下笔如有神”,这是古人关于读书的成功经验.开展课外阅读可以引起学生浓厚的学习兴趣和探求知识的强烈欲望,丰富知识,开阔视野,也有利于学习和巩固老师在课堂上所教的基础知识,使学生学得有趣,学得扎实,学得活泼,是启发智慧和锻炼才能的一条重要途径.为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,扩大知识源,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动,活动前对本校学生进行了“你最喜欢的图书类型(只写一项)”的随机抽样调查,相关数据统计如下:

请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整,并求出扇形统计图中小说所对应的圆心角度数.
(3)已知该校共有学生800人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长均为l的小正方形网格纸中,△ABC的顶点,A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上.

(1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧;
(2)分别写出B1、C1的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.

小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成相应的任务.
我们知道,二元一次方程有无数个解.在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如:![]() ,方程x﹣y=﹣1的一个解,对应点为(1,2).
,方程x﹣y=﹣1的一个解,对应点为(1,2).
我们在平面直角坐标系中标出,另外方程x﹣y=﹣1的解还对应点(2,3),(3,4)…将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程x﹣1=﹣1的解,所以,我们就把这条直线叫做方程x﹣y=﹣1的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.那么每个二元一次方程组应该对应两条直线,解这个方程组,相当于确定两条直线交点的坐标.
(1)已知A(1,1),B(﹣3,4),C(,2),则点 (填“A”、”B”、“C”)在方程2x﹣y=﹣1的图象上;
(2)求方程2x+3y=9和方程3x﹣4y=5图象的交点坐标.

查看答案和解析>>
科目: 来源: 题型:
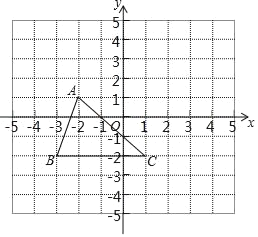
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'
(1)在图中画出△A′B′C';
(2)写出A',B'的坐标;
(3)求出△COC′的面积;
(4)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 的边长为6个单位长度,点
的边长为6个单位长度,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按![]() 的方向运动,再次回到
的方向运动,再次回到![]() 点结束运动,设
点结束运动,设![]() 点运动的时间为
点运动的时间为![]() 秒.
秒.

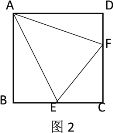

(1)如图1,若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
(2)如图2,若点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,点![]() 是对角线
是对角线![]() 的三等分点,且
的三等分点,且![]() ,若
,若![]() ,直接写出满足条件的
,直接写出满足条件的![]() 点的个数,并注明这些
点的个数,并注明这些![]() 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
查看答案和解析>>
科目: 来源: 题型:
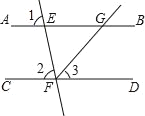
【题目】学习完第五章《相交线与平行线》后,王老师布置了一道儿何证明题如下:“如图,已知直线AB,CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.”善于动脑的小军快速思考,找到了解题方案,并书写出了如下不完整的解题过程.请你将该题解题过程补充完整:
解:∵∠1=∠2=80°(已知)
∴AB∥CD
∴∠BGF+∠3=180°
∵∠2+∠EFD=180°(邻补角的定义),
∴∠EFD= °(等式性质)
∵FG平分∠EFD(已知),
∴∠EFD=2∠3(角平分线的定义)
∴∠3= °(等式性质)
∴∠BGF= °(等式性质)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com