
科目: 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目: 来源: 题型:
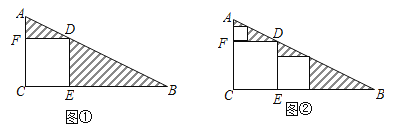
【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求![]() 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点P.
(1)以A点为位似中心,将△ABC在网格中放大成△AB1C1,使![]() =2,请画出△AB1C1;
=2,请画出△AB1C1;
(2)以P点为三角形的一个顶点,请画一个格点△PMN,使△PMN∽△ABC,且相似比为![]() .
.
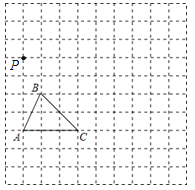
查看答案和解析>>
科目: 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学;
(2)条形统计图中,m,n的值;
(3)扇形统计图中,求出艺术类读物所在扇形的圆心角的度数;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校应购买其他类读物多少册?
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目: 来源: 题型:
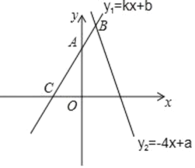
【题目】一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
查看答案和解析>>
科目: 来源: 题型:
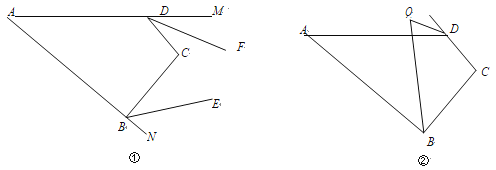
【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】花香村计划改造一片林地,估计这片林地可种梨树80~133棵.根据经验,若种100棵树,果树成熟后平均每棵树上能结500个梨,在这个基础上每多种一棵梨树,平均每棵会少结3个梨,每少种一棵,平均每棵树会多结4个梨.
(1)如果种植110棵梨树,则总共能结多少个梨?
(2)设种植x棵梨树,总共能结y个梨,
①当80≤x≤100时,求出y与x之间的函数关系式;
②当100<x≤134时,求出y与x之间的函数关系式;
(3)种多少棵梨树,总共能结的梨数最多?最多是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
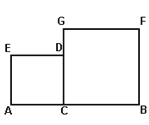
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com