
科目: 来源: 题型:
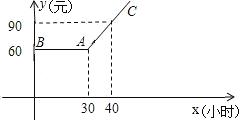
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】![]() .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=![]() .
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了更好治理某湖水质,保护环境,市治污公司决定购买![]() 台污水处理设备.现有
台污水处理设备.现有![]() ,
,![]() 两种型号的设备,其中每台的价格,月处理污水量如下表.经调查:购买一台
两种型号的设备,其中每台的价格,月处理污水量如下表.经调查:购买一台![]() 型设备比购买一台
型设备比购买一台![]() 型设备多
型设备多![]() 万元,购买
万元,购买![]() 台
台![]() 型设备比购买
型设备比购买![]() 台
台![]() 型设备少
型设备少![]() 万元.
万元.
|
| |
价格(万元/台) |
|
|
处理污水量(吨/月) |
|
|
(![]() )求
)求![]() ,
,![]() 的值.
的值.
(![]() )经预算:市治污公司购买污水处理设备的资金不超过
)经预算:市治污公司购买污水处理设备的资金不超过![]() 万元,你认为该公司有哪几种购买方案.
万元,你认为该公司有哪几种购买方案.
(![]() )在(
)在(![]() )问的条件下,若每月要求处理该湖的污水量不低于
)问的条件下,若每月要求处理该湖的污水量不低于![]() 吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
(1)若点P、Q均以3cm/s的速度移动,则:AP= cm;QC= cm.(用含t的代数式表示)
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间PD=PQ,使△DPQ为等腰三角形?
(3)若点P、Q均以3cm/s的速度移动,经过多长时间,四边形BPDQ为菱形?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目: 来源: 题型:
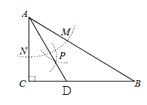
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com