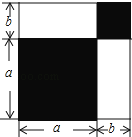
（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；

（2）由（1），你能得到怎样的等量关系？请用等式表示；

（3）如果图中的a，b（a＞b）满足a2+b2=53，ab=14，求：①a+b的值；②a4﹣b4的值．

【题目】阅读下列材料，完成相应的任务；全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时，我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”，进行了如下思考:如图1，四边形和四边形中，连接对角线，这样两个四边形全等的问题就转化为“”与“”的问题。若先给定“”的条件，只要再增加个条件使“”即可推出两个四边形中“四条边分别相等、四个角也分别和等”，从而说明两个四边形全等。

按照智慧小组的思路，小明对图中的四边形与四边形先给出和下条件: ,，小亮在此基础上又给出“”两个条件.他们认为满足这五个条件能得到“四边形四边形”.

（1）请根据小明和小亮给出的条件，说明“四边形四边形”的理由；

（2）请从下面两题中任选一题作答，我选择 题.

在材料中“小明所给条件”的基础上，小颖又给出两个条件“”.满足这五个条件 （填“能”或“不能”）得到四边形四边形

在材料中“小明所给条件的基础上”，再添加两个关于原四边形的条件（要求：不同于小亮的条件），使四边形四边形，你添加的条件是① ，② .

【题目】如图，在正方形中，边长为的等边三角形的顶点分别在边和上．

（1）判断的形状，并说明理由；

（2）求的长；

（3）试求正方形的面积．

（1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

（2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

(1) 4(x－2)2－36＝0；

(2) x2＋6x＋9＝25；

(3) 4(3x－1)2－9(3x＋1)2＝0.

【题目】为落实“美丽抚顺”的工作部署，市政府计划对城区道路进行了改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的倍，甲队改造360米的道路比乙队改造同样长的道路少用3天．

（1）甲、乙两工程队每天能改造道路的长度分别是多少米？

（2）若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1200米，改造总费用不超过145万元，至少安排甲队工作多少天？

（1）若∠A＝40°，求∠DBC的度数；

（2）若AE＝6，△CBD的周长为20，求BC的长．

（1）利用网格画出直角坐标系（要求标出x轴，y轴和原点），则点A的坐标为_________；

（2）以△ABC为基本图形，利用旋转设计一个图案，说明你的创意为__________________．

数学课上，老师让同学们利用三角形纸片进行操作活动，探究有关线段之间的关系.

问题情境：

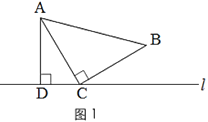
如图1，三角形纸片ABC中，∠ACB＝90°，AC＝BC.将点C放在直线l上，点A，B位于直线l的同侧，过点A作AD⊥l于点D.

初步探究：

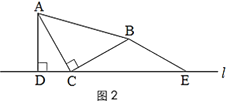
(1)在图1的直线l上取点E，使BE＝BC，得到图2.猜想线段CE与AD的数量关系，并说明理由；

变式拓展：

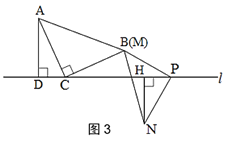
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作，其中∠MPN＝90°，MP＝NP.小颖在图 1 的基础上，将三角形纸片MPN的顶点P放在直线l上，点M与点B重合，过点N作NH⊥l于点 H.

请从下面 A，B 两题中任选一题作答，我选择_____题.

A.如图3，当点N与点M在直线l的异侧时，探究此时线段CP，AD，NH之间的数量关系，并说明理由.

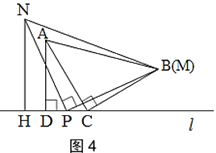
B.如图4，当点N与点M在直线l的同侧，且点P在线段CD的中点时，探究此时线段CD，AD，NH之间的数量关系，并说明理由.