
科目: 来源: 题型:
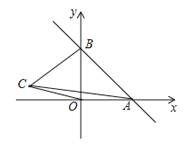
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目: 来源: 题型:
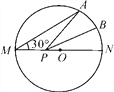
【题目】如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
A. 4![]() B. 2 C. 4 D. 2
B. 2 C. 4 D. 2![]()
查看答案和解析>>
科目: 来源: 题型:
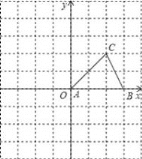
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
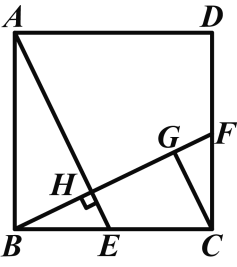
【题目】如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1)CG=BH;
(2)FC2=BF·GF;
(3)![]() .
.
查看答案和解析>>
科目: 来源: 题型:
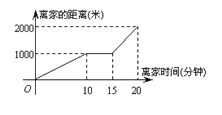
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,如图所示是小明从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
(1)小明从家到学校的路程共 米,从家出发到学校,小明共用了 分钟;
(2)小明修车用了多长时间?
(3)小明修车以前和修车后的平均速度分别是多少?
查看答案和解析>>
科目: 来源: 题型:
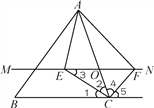
【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连结AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
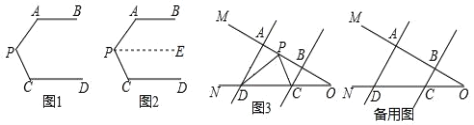
【题目】(1)如图1,AB∥CD,∠PAB=120°,∠PCD=110°,求∠APC的度数.小颖同学的解题思路是:如图2,过点P作PE∥AB,请你接着完成解答;如图3,点A、B在射线OM上,点C、D在射线ON上,AD∥BC,点P在射线OM上运动(点P与A、B、O三点不重合).
(2)当点P在线段AB上运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由;
(3)当点P在线段AB外运动时,判断∠CPD与∠ADP、∠BCP之间的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
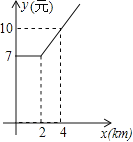
【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
查看答案和解析>>
科目: 来源: 题型:
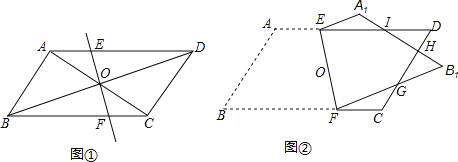
【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com